 |
A P. 5680. feladat (2025. november) |
P. 5680. Amikor a \(\displaystyle 30^\circ\)-os hajlásszögű, vízszintes síkban folytatódó domboldalt mindenütt hó borította, Peti szokatlan módját választotta a szánkózásnak: az emelkedő aljától számított 5 m távolságból különböző kezdősebességgel indult el.
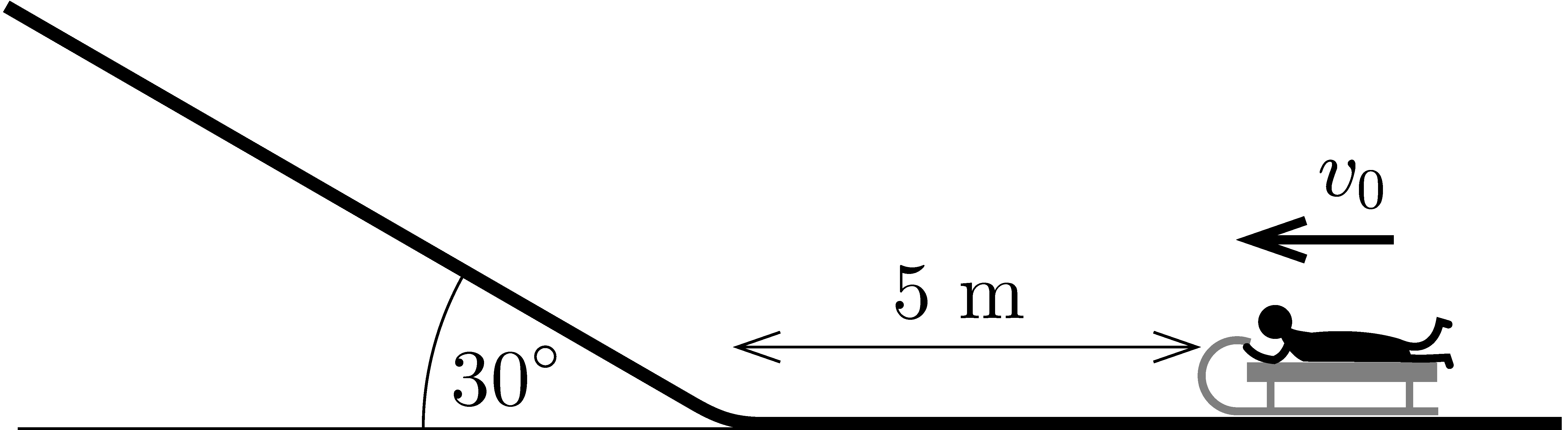
a) Mekkora kezdősebesség esetében áll meg leghamarabb a szánkó?
b) Milyen hosszú utat tett meg felfelé az emelkedőn ebben az esetben a szánkó?
A szánkó pályája egybeesett a domboldal esésvonalával. A lejtő töréspontmentesen csatlakozik a vízszintes felülethez. A szánkó és a hó között a súrlódás elhanyagolható.
Tornyai Sándor fizikaverseny, Hódmezővásárhely
(4 pont)
A beküldési határidő 2025. december 15-én LEJÁRT.
Megoldás. a) A szánkó a lejtő aljáig egyenletes sebességgel halad, a lejtőn pedig egyenletesen lassulva mozog a megállásig. A megállásig eltelő idő ennek a két időnek az összege:
\(\displaystyle t=\frac{d}{v}+\frac{v}{a},\)
ahol \(\displaystyle d=5\,\mathrm{m}\) a vízszintes szakasz hossza és \(\displaystyle a=g\sin 30^\circ\approx 5\,\mathrm{m/s^2}\) a szánkó gyorsulásának abszolút értéke.
A kifejezés minimumát a számtani és mértani közepek közötti egyenlőtlenség alapján határozhatjuk meg:
\(\displaystyle t=\frac{d}{v}+\frac{v}{a}\geq 2\sqrt{\frac{d}{v}\frac{v}{a}}=2\sqrt{\frac{d}{a}}\approx 2\,\mathrm{s}.\)
A kifejezés a minimumát akkor veszi fel, ha
\(\displaystyle \frac{d}{v}=\frac{v}{a},\)
amiből a keresett sebesség:
\(\displaystyle v=\sqrt{ad}\approx 5\,\mathrm{\frac{m}{s}}.\)
Megjegyzés. A minimumhely megkereshető deriválással vagy a kifejezés grafikonjának ábrázolásával is.
b) A vizsgált esetben a szánkó ugyanannyi ideig mozog a lejtőn, mint a vízszintes szakaszon, de az átlagos sebessége a lejtőn éppen fele akkora, mint a vízszintes talajon. Így a lejtőn fele akkora utat fog megtenni, mint a vízszintes szakaszon:
\(\displaystyle s=\frac{d}{2}=2{,}5\,\mathrm{m}.\)
Megjegyzés. Az út természetesen kiszámolható a gyorsulás, sebesség és időadatok közül bármely kettővel is:
\(\displaystyle s=\frac{v^2}{2a}=\frac{ad}{2a}=\frac{d}{2},\qquad s=\frac{t_\mathrm{min}}{2}\frac{v}{2}=\sqrt{\frac{d}{a}}\frac{\sqrt{ad}}{2}=\frac{d}{2},\qquad s=\frac{a}{2}\left(\frac{t_\mathrm{min}}{2}\right)^2=\frac{a}{2}\frac{d}{a}=\frac{d}{2}.\)
Statisztika:
53 dolgozat érkezett. 4 pontot kapott: Bense Tamás, Blaskovics Ádám, Bogdán Balázs Ákos, Bús László Teodor, Ferencz Kevin, Fuchs Vince, Gilyán Zsombor, Gönczi Botond, Halmosi Dávid, Horváth Péter, Kádár Luca Linda, Kossár Benedek Balázs, Kovács Tamás , Lakatos Levente, Magyar Levente Árpád, Mészáros Máté , Mezei Marcell, Misik Balázs, Molnár Lili, Monori Bence, Papp Emese Petra, Patócs 420 Péter, Rajtik Sándor Barnabás, Simon János Dániel, Tóth Hanga Katalin, Vértesi Janka, Vincze Anna, Winhoffer Júlia, Zádori Gellért, Zólomy Csanád Zsolt. 3 pontot kapott: Csáti Ambrus, Hornok Máté, Kirschner Bálint, Kovács Tamás, Mi Feiyu, Murányi Nimród Máté, Sofró Dániel, Szécsi Bence, Tasnádi Zsófia, Toók Panna, Török Tibor, Vigh István Csaba, Zhao Aaron . 2 pontot kapott: 2 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2025. novemberi fizika feladatai

