 |
A P. 5681. feladat (2025. november) |
P. 5681. Két darab, egyenként \(\displaystyle L=10~\mathrm{cm}\) hosszúságú fonal egy-egy végét közös pontban egy függőleges tengelyhez rögzítettük, a másik végükre két egyforma, \(\displaystyle m\) tömegű és \(\displaystyle Q\) töltésű kicsiny gyöngyöt erősítettünk. Egyensúlyi állapotban a fonalak \(\displaystyle \varphi=30^\circ\)-os szöget zárnak be a függőlegessel. Ha a tengelyt egyenletesen forgatjuk, a gyöngyök az állandósult állapotban egyenletes körmozgással mozognak úgy, hogy a fonalak \(\displaystyle \alpha=45^\circ\)-os szöget zárnak be a forgástengellyel.
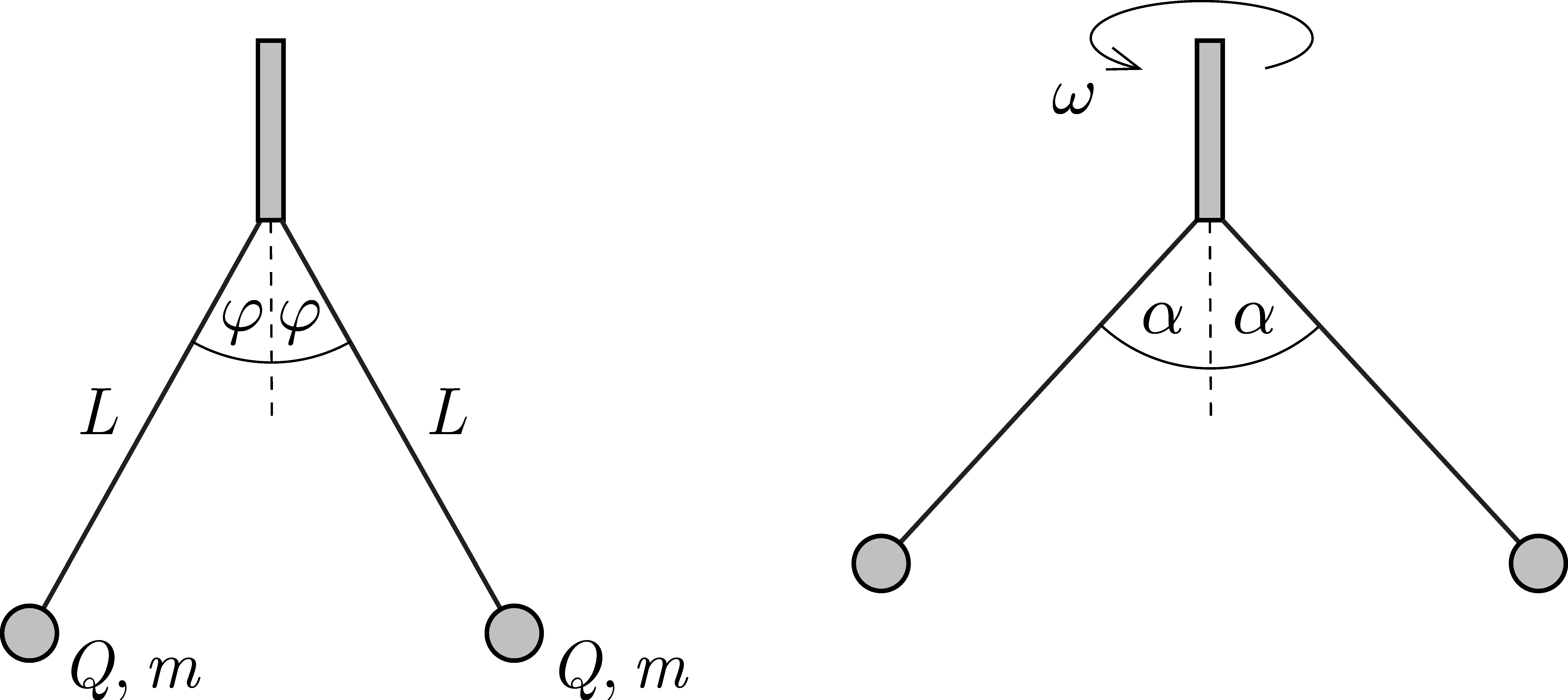
Mekkora a gyöngyök keringési ideje?
Közli: Zsigri Ferenc, Budapest
(4 pont)
A beküldési határidő 2025. december 15-én LEJÁRT.
Megoldás. Statikus egyensúly esetén a fonalakat valamekkora \(\displaystyle F_0\) erő feszíti, és a gyöngyökre a fonálerőkön kívül a függőleges irányú nehézségi erő és a vízszintes irányú Coulomb-erő hat. Az egyensúly feltétele az erőegyensúly:
\(\displaystyle \frac{kQ^2}{4L^2\sin^2\varphi}=F_0\sin\varphi,\)
valamint
\(\displaystyle mg=F_0\cos\varphi.\)
A fenti két egyenlet hányadosából
| \(\displaystyle (1)\) | \(\displaystyle \frac{kQ^2}{4L^2mg}=\frac{\sin^3\varphi}{\cos\varphi}.\) |
Jelöljük a forgó gyöngyök szögsebességét \(\displaystyle \omega\)-val, a keringési idejük ekkor \(\displaystyle T=2\pi/\omega.\) Ha a fonalakat feszítő erő most \(\displaystyle F_1\), a mozgásegyenletek:
| \(\displaystyle (2)\) | \(\displaystyle F_1\sin\alpha-\frac{kQ^2}{4L^2\sin^2\alpha}=m(L\sin\alpha)\omega^2,\) |
valamint
| \(\displaystyle (3)\) | \(\displaystyle mg=F_1\cos\alpha.\) |
Innen \(\displaystyle F_1\)-et kifejezve és azt (2)-be helyettesítve, valamint (1)-et is felhasználva kapjuk, hogy
| \(\displaystyle (4)\) | \(\displaystyle \frac{L\omega^2}{g}=\frac{1}{\cos\alpha}-\left(\frac{\sin\varphi}{\sin\alpha}\right)^3\,\frac{1}{\cos\varphi}.\) |
A megadott szögek esetén (4) jobb oldala \(\displaystyle 1{,}006\approx 1\), így a gyöngyök keringési ideje
\(\displaystyle T\approx 2\pi\sqrt{\frac{L}{g}}=0{,}63\,\mathrm{s},\)
ami majdnem az \(\displaystyle L\) fonálhosszúságú matematikai inga lengésidejével egyezik meg.
Statisztika:
47 dolgozat érkezett. 4 pontot kapott: Bense Tamás, Bogdán Balázs Ákos, Bús László Teodor, Csáki Anikó, Elekes Panni, Ferencz Kevin, Fuchs Vince, Gilyán Zsombor, Hornyák Zalán Zétény, Horváth Péter, Kossár Benedek Balázs, Kovács Tamás , Misik Balázs, Monori Bence, Murányi Nimród Máté, Papp Emese Petra, Simon János Dániel, Szabó Tamás, Tajta Sára, Tasnádi Zsófia, Tóth Hanga Katalin, Török Tibor, Vértesi Janka, Winhoffer Júlia, Zádori Gellért, Zhao Aaron . 3 pontot kapott: Blaskovics Ádám, Borsics Bendegúz, Hornok Máté, Kovács Tamás, Lakatos Levente, Mészáros Máté , Mezei Marcell, Molnár Lili, Nagy Gellért Ákos, Rajtik Sándor Barnabás, Sofró Dániel, Vincze Anna. 2 pontot kapott: 3 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2025. novemberi fizika feladatai

