 |
A P. 5682. feladat (2025. november) |
P. 5682. Egy \(\displaystyle R\) sugarú, \(\displaystyle H\) magasságú hengerben folyadék van. A hengert a tengelye körül forgásba hozzuk. A forgás szögsebességét lassan növeljük egészen addig, amíg a folyadék széle felhúzódik egészen az edény szájáig. Ekkor a pohár aljának közepéről éppen ,,eltűnik'' a folyadék.
a) Mekkora az edény legnagyobb szögsebessége?
b) Milyen magasan áll a folyadék a hengerben induláskor?
Közli: Simon Péter, Pécs
(5 pont)
A beküldési határidő 2025. december 15-én LEJÁRT.
Megoldás. A folyadék felszíne mindenhol merőleges a nehézségi erő és a forgó rendszerben érzékelt centrifugális erő eredőjére. Az 1. ábráról leolvasható, hogy az érintő meredeksége:
| \(\displaystyle (1)\) | \(\displaystyle \tg\alpha=\frac{\omega^2r}{g}.\) |
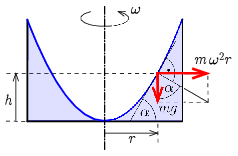
1. ábra
Emiatt a felület forgási paraboloid alakú lesz, melynek egyenlete:
| \(\displaystyle (2)\) | \(\displaystyle h=\frac{\omega^2}{2g}r^2,\) |
ahol \(\displaystyle r\) a forgástengelytől mért távolság, \(\displaystyle h\) a forgási paraboloid csúcsától mért magasság, \(\displaystyle \omega\) a forgás szögsebessége és \(\displaystyle g\) a nehézségi gyorsulás.
Megjegyzés. A forgó folyadék felszínének egyenlete ,,közismert'', megtalálható a Függvénytáblázatban is, de ezen kívül többféleképpen is levezethető. Itt egy geometriai és egy differenciálszámításos módszert mutatunk meg.
1. A parabolatükör a tengelyével párhuzamos fénysugarakat a fókuszpontba gyűjti (2. ábra). A parabola geometriai definíciója szerint a fókuszponttól és a vezéregyenestől egyenlő távolságra lévő pontok halmaza (\(\displaystyle PF=PP'\)). Az \(\displaystyle F\) fókuszpont és a \(\displaystyle v\) vezéregyenes távolsága a parabola \(\displaystyle p\) paramétere, amellyel a parabola egyenlete:
\(\displaystyle h=\frac{1}{2p}r^2.\)
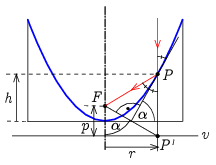
2. ábra
Az 2. ábráról leolvashatóan a görbe érintője az \(\displaystyle FPP'\) egyenlőszárú háromszög szimmetriatengelye, így az \(\displaystyle FP'\) szakasz merőleges rá. Ezért a merőlegesállású szögek miatt:
\(\displaystyle \tg\alpha=\frac{r}{p}.\)
Ezek alapján (1) felhasználásával:
$$\begin{gather*} p=\frac{r}{\tg\alpha}=\frac{g}{\omega^2},\\ h=\frac{1}{2p}r^2=\frac{\omega^2}{2g}r^2, \end{gather*}$$a (2) kifejezéssel összhangban.
2. A \(\displaystyle h(r)\) függvény meredeksége (1) alapján:
\(\displaystyle \frac{\mathrm{d}h}{\mathrm{d}r}=\tg\alpha=\frac{\omega^2r}{g}.\)
Ebből
\(\displaystyle \mathrm{d}h=\frac{\omega^2}{g}r\,\mathrm{d}r,\)
és ezt integrálva
\(\displaystyle h=\frac{\omega^2}{2g}r^2+h_0.\)
\(\displaystyle h_0=0\) választással megkapjuk a (2) összefüggést.
A feladatban keresett határesetben a forgási paraboloid érinti az edény fenekét és felső határolóköre megegyezik az edény peremével, így \(\displaystyle h(R)=H\):
\(\displaystyle \frac{\omega^2}{2g}R^2=H,\)
amiből
\(\displaystyle \omega=\frac{\sqrt{2gH}}{R}.\)
b) Az eredeti magasság meghatározásához ki kell számítanunk a folyadék térfogatát. Ehelyett az egyszerűség kedvéért a folyadék nélküli forgási paraboloid térfogatát számítjuk ki (a 3. ábrán piros). A kis szelet térfogata:
\(\displaystyle \mathrm{d}V=r^2\pi\,\mathrm{d}h.\)
A parabola egyenlete a peremfeltételek alapján:
\(\displaystyle h=\frac{H}{R^2}r^2,\)
amellyel a kis elemi térfogat így is írható:
\(\displaystyle \mathrm{d}V=\frac{R^2\pi}{H}h\,\mathrm{d}h.\)
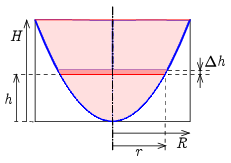
3. ábra
A teljes térfogat egyszerű integrálással:
\(\displaystyle V=\int\limits_0^H\frac{R^2\pi}{H}h\,\mathrm{d}h=\frac{R^2\pi}{H}\frac{H^2}{2}=\frac{HR^2\pi}{2}.\)
Ez éppen a henger \(\displaystyle HR^2\pi\) térfogatának a fele, így a folyadék térfogata is ugyanekkora. Eszerint kezdetben a folyadékszint \(\displaystyle H/2\) magasságban volt.
Megjegyzés. A folyadék térfogata a forgástestek térfogatszámítási módszerével is meghatározható. Ekkor a forgástestet \(\displaystyle r\) sugarú, \(\displaystyle \mathrm{d}r\) vastagságú, \(\displaystyle h(r)\) magasságú hengergyűrűkre bontjuk (4. ábra), melyek térfogata:
\(\displaystyle \mathrm{d}V=2r\pi h(r)\,\mathrm{d}r.\)
Behelyettesítve \(\displaystyle h(r)\) aktuális kifejezését, és az integrálást elvégezve:
\(\displaystyle V=\int\limits_0^R\frac{2H\pi}{R^2}r^3\,\mathrm{d}r=\frac{2H\pi}{R^2}\frac{R^4}{4}=\frac{HR^2\pi}{2},\)
az előző eredményünkkel összhangban.
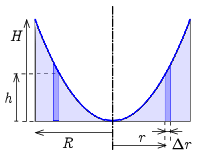
4. ábra
Statisztika:
39 dolgozat érkezett. 5 pontot kapott: Beke Márton Csaba, Bogdán Balázs Ákos, Csáki Anikó, Elekes Panni, Erdélyi Dominik, Gyenes Károly, Halmosi Dávid, Kovács Tamás, Nyitrai Csenger, Rajtik Sándor Barnabás, Simon János Dániel, Szécsi Bence, Tasnádi Zsófia, Tóth Hanga Katalin, Török Tibor, Vigh István Csaba, Winhoffer Júlia, Zhao Aaron . 4 pontot kapott: Bense Tamás, Hajdu Eszter, Kovács Tamás , Mezei Marcell, Monori Bence, Patócs 420 Péter, Szabó Tamás, Zádori Gellért, Zólomy Csanád Zsolt. 3 pontot kapott: 3 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 3 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2025. novemberi fizika feladatai

