 |
A P. 5684. feladat (2025. november) |
P. 5684. Egyenletes vastagságú drótból az ábrán látható keretet készítjük el. Számítsuk ki az \(\displaystyle A\) és \(\displaystyle B\), valamint az \(\displaystyle A\) és \(\displaystyle C\) pontok közötti eredő ellenállások arányát!
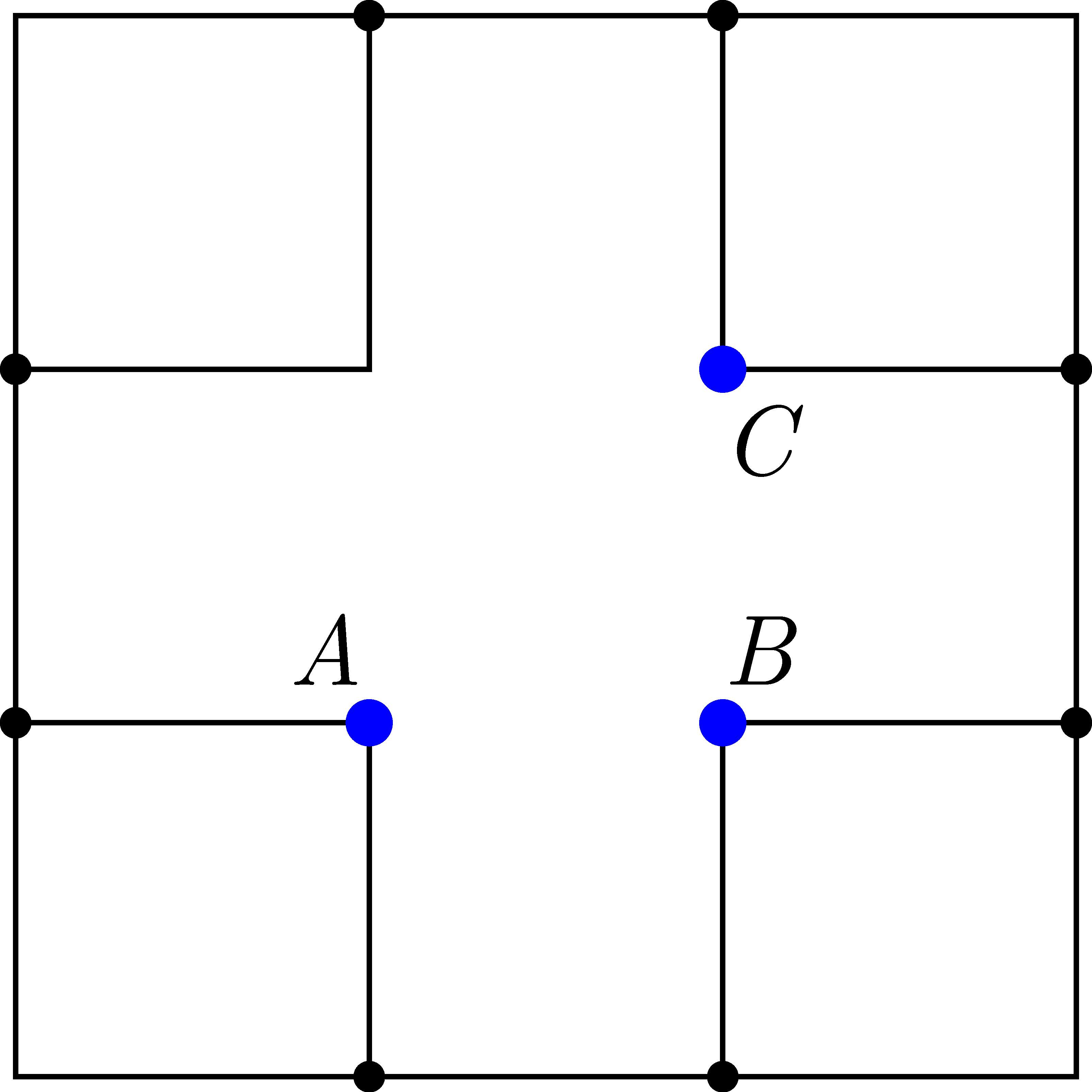
Közli: Cserti József, Budapest
(5 pont)
A beküldési határidő 2025. december 15-én LEJÁRT.
Megoldás. Először is rajzoljuk át a kapcsolási rajzot úgy, hogy a sorosan és párhuzamosan kapcsolt részek áttekinthetőbbek legyenek. Az 1. ábrán a nagy négyzeten további pontokat jelöltünk meg, hogy segítsük a kétféle elrendezés részleteinek azonosítását. A 2. ábrán \(\displaystyle A\) és \(\displaystyle C\), a 3. ábrán \(\displaystyle A\) és \(\displaystyle B\) a kapcsolás kimeneti pontjai. Ellenállásegységnek a kicsi négyzet egyik oldalának \(\displaystyle R\) ellenállását választottuk; a jelöletlen ellenállások 1 egységnyiek.
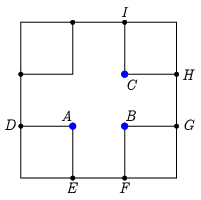
1. ábra
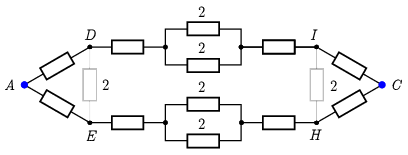
2. ábra
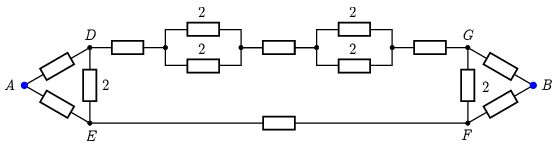
3. ábra
Kezdjük az \(\displaystyle A\) és \(\displaystyle C\) pontok közti \(\displaystyle R_{AC}\) eredő ellenállással (2. ábra). A kapcsolás alsó és felső ága egyforma, a két függőleges helyzetben (halványabban) rajzolt ellenállás végpontjai azonos potenciálon vannak, nem folyik rajtuk áram, ezért olyan, mintha ott sem lennének. Nélkülük a kapcsolás csak soros és párhuzamos részekből áll, az eredő ellenállás pedig:
\(\displaystyle R_{AC}=\frac{1}{2}\left(R+R+\frac{1}{2}\cdot 2R+R+R\right)=2{,}5R.\)
A 3. ábrán látható kapcsolás kicsit bonyolultabb: az alsó és felső ág különbözik, és a függőleges ágakban is folyik áram. Hogy az ezzel járó bonyodalmakat elkerüljük, alakítsuk a szélen levő háromszögeket csillaggá (\(\displaystyle \Delta\)-t Y-ná) úgy, ahogy a 4. ábrán látható.

4. ábra
A csillagban levő ellenállások értékeit a Függvénytáblázatban található képletek segítségével kaptuk:
\(\displaystyle \frac{R\cdot R}{R+R+2R}=\frac{1}{4}R,\qquad\frac{R\cdot 2R}{R+R+2R}=\frac{1}{2}R.\)
A \(\displaystyle D\) és \(\displaystyle G\) pontok közti rész eredő ellenállása:
\(\displaystyle R_{DG}=R+\frac{1}{2}\cdot 2R+R+\frac{1}{2}\cdot 2R+R=5R.\)
Az utolsó két eredményt berajzolva a 3. ábrába az 5. ábrához jutunk, melynek eredő ellenállását már könnyebben felírhatjuk:
\(\displaystyle R_{AB}=\frac{1}{4}R+\frac{\left(\frac{1}{2}R+5R+\frac{1}{2}R\right)\left(\frac{1}{2}R+R+\frac{1}{2}R\right)}{\left(\frac{1}{2}R+5R+\frac{1}{2}R\right)+\left(\frac{1}{2}R+R+\frac{1}{2}R\right)}+\frac{1}{4}R=\frac{1}{2}R+\frac{6R\cdot 2R}{8R}=2R\)
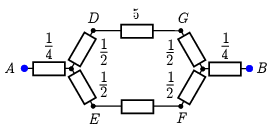
5. ábra
A két eredő ellenállás aránya végül:
\(\displaystyle \frac{R_{AB}}{R_{AC}}=\frac{2R}{2{,}5R}=\frac{4}{5}=0{,}8.\)
Statisztika:
32 dolgozat érkezett. 5 pontot kapott: Bense Tamás, Bogdán Balázs Ákos, Erdélyi Dominik, Ferencz Kevin, Kovács Tamás, Molnár Lili, Rajtik Sándor Barnabás, Simon János Dániel, Sipeki Andor, Török Tibor, Zádori Gellért. 4 pontot kapott: Kovács Dániel, Patócs 420 Péter, Zólomy Csanád Zsolt. 3 pontot kapott: 6 versenyző. 2 pontot kapott: 5 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2025. novemberi fizika feladatai

