 |
A P. 5687. feladat (2025. november) |
P. 5687. Négy darab, \(\displaystyle r\) sugarú, \(\displaystyle m\) tömegű golyót \(\displaystyle r\) hosszúságú, vékony fonalakkal kötünk fel egy közös pontba úgy, hogy a golyók középpontja egy négyzetet határozzon meg. A négyzet egyik átlójának végén lévő két golyó piros, a másik kettő kék színű. (A golyók tömegének legnagyobb része a golyó középpontjánál található, emiatt a golyók tehetetlenségi nyomatéka elhanyagolhatóan kicsi. Ugyancsak elhanyagolható a golyók közötti súrlódási erő is.)
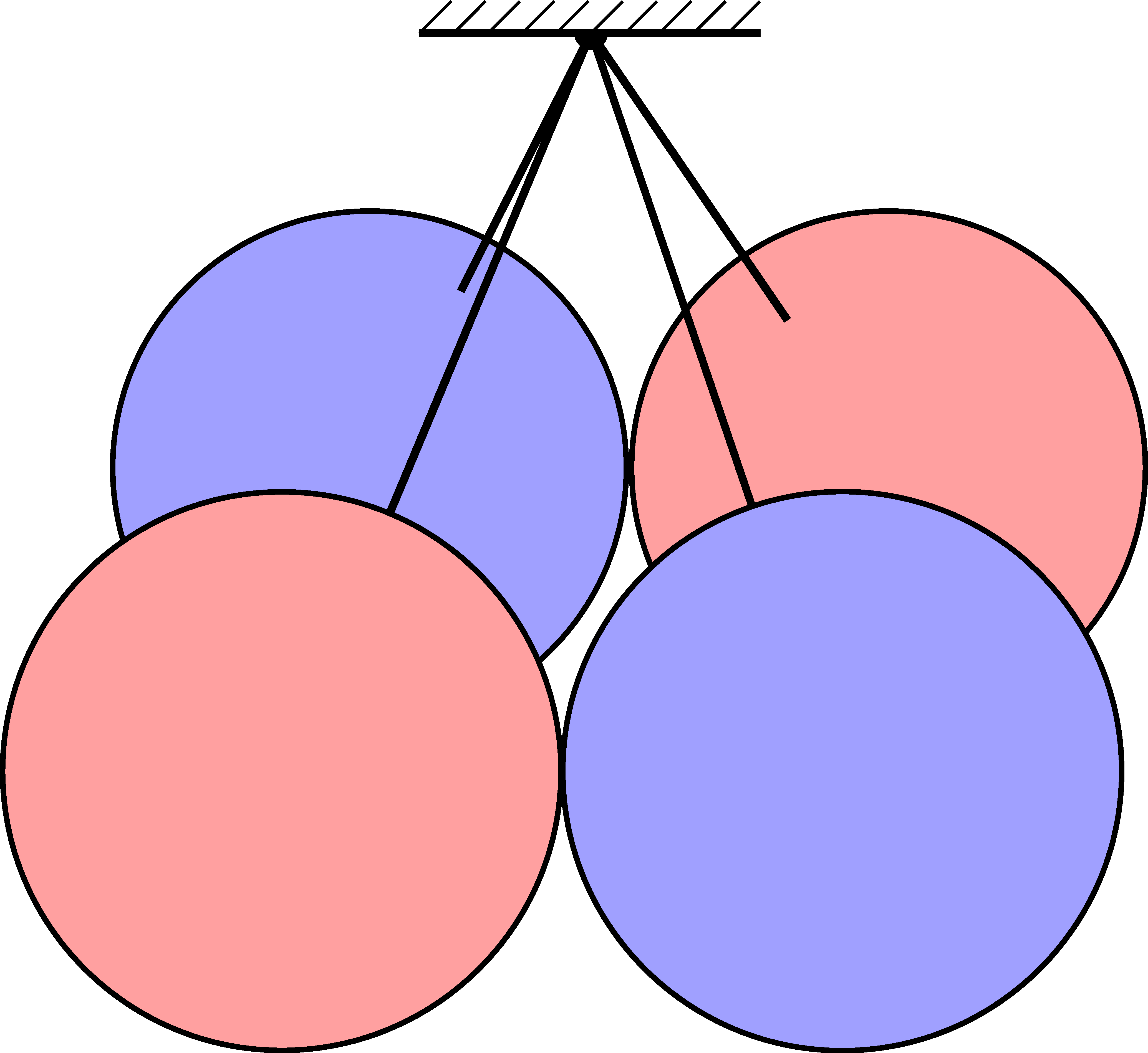
A golyók ilyen elrendeződése instabil egyensúlyi helyzet, amiből a rendszer a legkisebb külső zavar hatására ,,kibillen'', és egyre gyorsuló mozgással egy alacsonyabb helyzeti energiájú állapot felé mozdul el.
a) Mekkora szöget zárnak be a függőlegessel a fonalak a kezdeti, illetve a legkisebb helyzeti energiájú állapotban?
b) Mekkora a négy golyó összes mozgási energiájának legnagyobb értéke?
Közli: Kis Tamás (Heves), Gnädig Péter (Vácduka)
(6 pont)
A beküldési határidő 2025. december 15-én LEJÁRT.
Megoldás. A golyók nullának vehető tehetetlenségi nyomatéka miatt az egyes fonalak meghosszabbítása a golyó középpontján kell, hogy áthaladjon. (Ha nem így lenne, akkor a fonalat feszítő erőnek lenne forgatónyomatéka a golyó középpontja körül, és ez nagyon (,,végtelen'') nagy szöggyorsulást eredményezne.)
Mind a négy golyó középpontja a mozgás során mindvégig \(\displaystyle 2r\) távolságban lesz a közös felfüggesztési ponttól. Válasszunk egy olyan koordináta-rendszert, amelynek egy-egy vízszintes tengelye az instabil kezdeti állapot négyzetének átlóival párhuzamos, a harmadik tengely pedig a felfüggesztési ponton áthaladó függőleges egyenes. Jelöljük az \(\displaystyle x-z\) síkban kitérített piros golyók fonalainak a függőlegessel bezárt szögét \(\displaystyle \alpha\)-val, a másik két fonál szögét pedig \(\displaystyle \beta\)-val (lásd az ábrát). Az első felülnézeti ábrarészlet a négyzet alaknak megfelelő kezdeti állapotot mutatja. A második felülnézeti és a két oldalnézeti ábrarészlet olyan helyzetet mutat, amikor a két piros golyó egymáshoz közelebb került (és emiatt függőlegesen kicsit lesüllyedtek), a kék golyók pedig eltávolodtak egymástól (miközben a középpontjuk kicsit megemelkedett). Ilyen elmozdulás során a piros golyók helyzeti energiája csökken, a kékeké pedig növekszik. Kérdés, hogy az egész rendszer helyzeti energiája kisebb-e, mint amennyi a kezdeti állapotban volt. Ha kisebb, akkor a kezdőállapot valóban instabil egyensúlyi állapot.
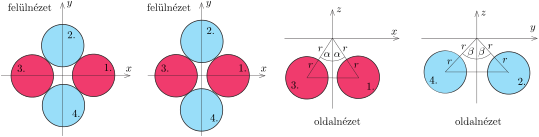
Ha a koordináta-rendszer kezdőpontját a közös felfüggesztési pontba helyezzük, akkor a golyók középpontját megadó vektorok
\(\displaystyle \boldsymbol{r}_{1,3}=\left(\begin{matrix}\pm 2r\sin\alpha&\\0&\\-2r\cos\alpha&\end{matrix}\right)\qquad\textrm{és}\qquad\boldsymbol{r}_{2,4}=\left(\begin{matrix}0&\\ \pm 2r\sin\beta&\\-2r\cos\beta&\end{matrix}\right).\)
Az egymással érintkező (különböző színű) golyók középpontjának távolsága \(\displaystyle 2r\), így pl.
\(\displaystyle \left(\boldsymbol{r}_1-\boldsymbol{r}_2\right)^2=(2r\sin\alpha)^2+(2r\sin\beta)^2+4r^2(\cos\alpha-\cos\beta)^2=4r^2,\)
vagyis
| \(\displaystyle (1)\) | \(\displaystyle \cos\alpha\cdot\cos\beta=\frac{1}{2}.\) |
a) A kezdőállapotban (a négyzetes elrendeződésben)
\(\displaystyle \cos\alpha=\cos\beta=\frac{1}{\sqrt{2}},\qquad\textrm{vagyis}\qquad\alpha=\beta=45^\circ.\)
Az \(\displaystyle \alpha\) szög legkisebb értékénél a piros golyók érintkeznek egymással, ilyenkor
| \(\displaystyle (2)\) | \(\displaystyle \sin\alpha_\mathrm{min}=\frac{1}{2},\qquad\cos\alpha_\mathrm{min}=\frac{\sqrt{3}}{2},\qquad\alpha_\mathrm{min}=30^\circ.\) |
A kék golyókat tartó fonalaknak a függőlegessel bezárt legnagyobb szögére (1) és (2) szerint fennáll:
| \(\displaystyle (3)\) | \(\displaystyle \cos\beta_\mathrm{max}=\frac{1}{\sqrt{3}},\qquad\textrm{azaz}\qquad\beta_\mathrm{max}\approx 54{,}7^\circ.\) |
b) Az egész rendszer helyzeti energiája
\(\displaystyle E_\mathrm{helyzeti}=-4mgr(\cos\alpha+\cos\beta)=-4mgr\left(\cos\alpha+\frac{1}{2\cos\alpha}\right)=\)
\(\displaystyle =-4mgr\left(\sqrt{\cos\alpha}-\frac{1}{\sqrt{2\cos\alpha}}\right)^2-4\sqrt{2}\,mgr\leq -4\sqrt{2}mgr.\)
Látjuk, hogy a helyzeti energia az \(\displaystyle \alpha=\beta=45^\circ\)-os helyzetben, vagyis a kezdeti (négyzetes szimmetriát mutató) állapotban a legnagyobb, ez tehát egy instabil egyensúlyi helyzet.
A helyzeti energia függvénye a legkisebb értéket a piros (vagy a kék) golyók összeütközésekor, \(\displaystyle \alpha=30^\circ\), \(\displaystyle \beta=54{,}7^\circ\)-nál (vagy a fordított helyzetben, a kék golyók összeütközésekor) veszi fel, és a nagysága
\(\displaystyle E_\textrm{h,min}=-\frac{10}{\sqrt{3}}mgr.\)
A rendszer helyzeti energiájának csökkenése a teljes folyamat során
\(\displaystyle \vert\varDelta E\vert=\left(\frac{10}{\sqrt{3}}-4\sqrt{2}\right)mgr\approx 0{,}12\,mgr,\)
legfeljebb ennyi lehet tehát a négy golyó összes mozgási energiája.
Statisztika:
19 dolgozat érkezett. 6 pontot kapott: Erdélyi Dominik, Patócs 420 Péter, Rajtik Sándor Barnabás, Simon János Dániel, Szécsi Bence, Tajta Sára. 5 pontot kapott: Nyitrai Csenger, Zádori Gellért. 4 pontot kapott: 3 versenyző. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 2 versenyző.
A KöMaL 2025. novemberi fizika feladatai

