 |
A P. 5688. feladat (2025. december) |
P. 5688. Egy adott pontból \(\displaystyle \alpha\) szög alatt \(\displaystyle v_0\) kezdősebességgel elhajítunk egy súlyos testet. Adjuk meg a pálya egyenletét abban a ferdeszögű koordináta-rendszerben, amelynek egyik tengelye a hajítás irányába, a másik pedig a nehézségi erő irányába mutat. Kapcsolatba hozható-e az egyenletben fellépő állandó a parabola alakú pályagörbe \(\displaystyle p\) ,,paraméterével''?
Példatári feladat nyomán
(4 pont)
A beküldési határidő 2026. január 15-én LEJÁRT.
Megoldás. Egy pontszerűnek tekinthető test mozgását az időtől függő \(\displaystyle \boldsymbol{r}(t)\) vektorral, vagyis egy skalár változós vektorfüggvénnyel írhatjuk le. Ha a mozgás síkbeli (ez a helyzet a hajításoknál), a helyvektor kifejezhető két tetszőleges (de egymással nem párhuzamos), időben állandó \(\displaystyle \boldsymbol{f}_1\) és \(\displaystyle \boldsymbol{f}_2\) ,,bázisvektor'' és az időtől függő két ,,koordináta'' segítségével:
\(\displaystyle \boldsymbol{r}(t)=X(t)\boldsymbol{f}_1+Y(t)\boldsymbol{f}_2.\)
Ha a bázisvektorok merőlegesek egymásra és egységnyi hosszúságúak, akkor a szokásos derékszögű (Descartes-féle) koordináta-rendszert kapjuk:
\(\displaystyle \boldsymbol{r}(t)=x(t)\boldsymbol{e}_1+y(t)\boldsymbol{e}_2.\)
(Az általános esettől való megkülönböztetés kiemelésére a bázisvektorokat \(\displaystyle \boldsymbol{e}_{1,2}\)-vel, a koordinátákat pedig kis betűkkel jelöltük.)
Válasszuk \(\displaystyle \boldsymbol{f}_1\)-nek az eldobás irányába mutató egységvektort, \(\displaystyle \boldsymbol{f}_2\)-nek pedig a nehézségi gyorsulás irányába (függőlegesen lefelé) mutató egységvektort. Ebben a ferdeszögű koordináta-rendszerben a mozgó test koordinátái az idő függvényében
\(\displaystyle X(t)=v_0t\qquad\textrm{és}\qquad Y(t)=\frac{g}{2}t^2.\)
Innen – az idő kiküszöbölése után – megkapjuk a pályagörbe egyenletét:
\(\displaystyle Y(X)=\frac{g}{2v_0^2}\,X^2.\)
Descartes-féle koordináta-rendszerben a parabola egyenletében a négyzetes tag együtthatója \(\displaystyle \frac{1}{2p}\), ahol \(\displaystyle p\) a fókuszpont és a vezéregyenes távolsága, vagyis a parabola paramétere. Jelen esetben mégsem mondhatjuk, hogy \(\displaystyle \frac{v_0^2}{g}\) megegyezne \(\displaystyle p\)-vel, hiszen a választott bázisvektorok (a vízszintes hajítás \(\displaystyle \alpha=0\), illetve \(\displaystyle \alpha=180^\circ\) eseteit leszámítva) nem merőlegesek egymásra. (Jól látható ez a függőleges hajítás \(\displaystyle \alpha\to 0\) határesetében, amikor a függőleges félegyeneshez közelítő ,,elfajult parabola'' paramétere nem \(\displaystyle v_0^2/g\)-hez, hanem nullához tart.)
Fejezzük ki most az \(\displaystyle \boldsymbol{r}\) vektort egy vízszintes \(\displaystyle \boldsymbol{e}_1\) és egy függőlegesen felfelé mutató \(\displaystyle \boldsymbol{e}_2\) egységvektor segítségével.
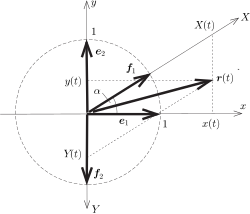
Az ábráról leolvasható, hogy
\(\displaystyle \boldsymbol{f}_1=\cos\alpha\,\boldsymbol{e}_1+\sin\alpha\,\boldsymbol{e}_2,\qquad\textrm{illetve}\qquad\boldsymbol{f}_2=-\boldsymbol{e}_2,\)
és így
\(\displaystyle \boldsymbol{r}(t)=X(t)\,(\cos\alpha\,\boldsymbol{e}_1+\sin\alpha\,\boldsymbol{e}_2)-Y(t)\,\boldsymbol{e}_2=\left(v_0t\cos\alpha\right)\,\boldsymbol{e}_1+\left(v_0t\sin\alpha-\frac{g}{2}t^2\right)\boldsymbol{e}_2.\)
Ezek szerint a helyvektor derékszögű koordinátái:
\(\displaystyle x(t)=v_0t\cos\alpha,\qquad\textrm{valamint}\qquad y(t)=v_0t\sin\alpha-\frac{g}{2}t^2,\)
vagyis a pályagörbe egyenlete
\(\displaystyle y(x)=x\,\tg\alpha-\frac{g}{2v_0^2\cos^2\alpha}\,x^2.\)
Innen – teljes négyzetté alakítás után – kapjuk, hogy a lefelé nyíló parabola paramétere
\(\displaystyle p=\frac{v_0^2\cos^2\alpha}{g}.\)
Statisztika:
17 dolgozat érkezett. 4 pontot kapott: Bogdán Balázs Ákos, Halmosi Dávid, Mezei Marcell, Patócs 420 Péter, Szécsi Bence, Tasnádi Zsófia. 3 pontot kapott: Kádár Luca Linda, Kovács Tamás , Magyar Levente Árpád, Nagy Gellért Ákos, Nyitrai Csenger, Papp Emese Petra, Vincze Anna, Winhoffer Júlia, Zádori Gellért, Zhao Aaron .
A KöMaL 2025. decemberi fizika feladatai

