A P. 5689. feladat (2025. december)

P. 5689. Tekintsük a Föld Nap körüli pályáját 150 millió kilométer sugarú körnek. Tegyük fel, hogy egy üstökös az ekliptika síkjában, parabolapályán közelít a Naphoz úgy, hogy a Föld pályáját kétszer metszi, és a két metszéspontot összekötő egyenes szakasz hossza éppen a földpálya átmérője. (Szerencsére a Föld jó messzire elkerüli az üstököst, amikor az a földpálya közelében mozog.)

a) Mennyire közel halad el az üstökös a Nap középpontjához, és mekkora a sebessége ekkor?

b) Mekkora szögben metszi egymást a Föld és az üstökös pályája?

Közli: Honyek Gyula, Veresegyház

(5 pont)

A beküldési határidő 2026. január 15-én LEJÁRT.

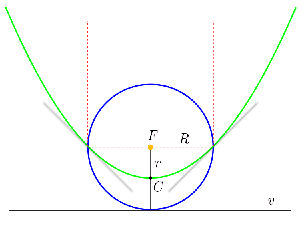
Megoldás. a) A földpálya középpontja egybeesik az üstökös parabolapályájának fókuszával. A parabola minden pontja ugyanakkora távolságra van az \(\displaystyle F\) fókusztól, mint a \(\displaystyle v\) vezéregyenestől. A két metszéspont éppen \(\displaystyle R\) földsugárnyira van a fókusztól, tehát ugyancsak \(\displaystyle R\) távolságra van a vezéregyenes is ezektől a pontoktól. Ebből következik, hogy a parabola vezéregyenese érinti a földpálya körét, és ezért a parabola \(\displaystyle C\) csúcspontja a földsugár felénél van, vagyis az üstökös \(\displaystyle r=R/2=75\) millió kilométerre közelíti meg a Napot. A parabolapálya miatt az üstökös teljes energiája nulla. Ebből ki tudjuk számítani az üstökös sebességét napközelben:

\(\displaystyle \frac{1}{2}mv^2-\gamma\frac{mM}{r}=0,\quad\textrm{amiből}\quad v=\sqrt{\frac{2\gamma M}{r}}=59{,}6\,\mathrm{km/s}.\)

b) Többféleképpen is megadhatjuk a választ. A legegyszerűbb talán az, ha optikai analógiát használunk. A parabola (térben forgási paraboloid) tengelyével párhuzamosan érkező fénysugarak úgy verődnek vissza a parabolatükörről, hogy azok a fókuszpontban koncentrálódnak. A két pálya metszéspontjaiba érkező, a parabola tengelyével párhuzamos sugarak eltérülése \(\displaystyle 90^\circ\)-os, tehát a két pálya \(\displaystyle 45^\circ\)-ban metszi egymást.

Statisztika:

38 dolgozat érkezett.
5 pontot kapott:	Bertollo Antonio, Elekes Panni, Erdélyi Dominik, Halmosi Dávid, Horváth Péter, Horváth Zsombor, Kádár Luca Linda, Kávrán-Kőnig Balázs, Kossár Benedek Balázs, Kovács Dániel, Kovács Tamás, Lakatos Levente, Nagy Gellért Ákos, Papp Emese Petra, Rajtik Sándor Barnabás, Simon János Dániel, Sümeghi Nándor , Szécsi Bence, Tajta Sára, Tóth Hanga Katalin, Török Tibor, Vértesi Janka, Vigh István Csaba, Winhoffer Júlia, Zádori Gellért, Zólomy Csanád Zsolt.
4 pontot kapott:	Bense Tamás, Gilyán Zsombor, Gombos Barna, Mezei Marcell.
3 pontot kapott:	2 versenyző.
1 pontot kapott:	1 versenyző.

A KöMaL 2025. decemberi fizika feladatai