 |
A P. 5690. feladat (2025. december) |
P. 5690. Egy \(\displaystyle \alpha\) hajlásszögű lejtőn \(\displaystyle G\) súlyú kicsiny test nyugszik. A test és a lejtő közötti tapadó súrlódás együtthatója \(\displaystyle \mu>\tg\alpha\).
Legalább mekkora nagyságú és milyen irányú erővel tudjuk a testet megmozdítani?
Közli: Gnädig Péter, Vácduka
(5 pont)
A beküldési határidő 2026. január 15-én LEJÁRT.
I. megoldás. Hihetőnek tűnik az a feltételezés, hogy a testet akkor tudjuk a legkisebb erővel megmozdítani, ha a lejtő esésvonala és a függőleges által meghatározott síkban lefelé, de nem az esésvonal irányába, hanem azzal valamekkora \(\displaystyle \varphi\) szöget bezáróan a lejtő síkjára merőlegesen is húzzuk. Ez utóbbi erőkomponens ugyanis csökkenti a lejtő és a test között kialakuló nyomóerőt, és így a tapadó súrlódási erő maximális értéke is lecsökken. Belátható (lásd II. és a III. megoldást), hogy ha a lejtő szintvonalaival párhuzamos, tehát ,,oldalirányú'' erőt is kifejtünk, a test megmozdításához szükséges minimális erő nagysága megnő.
A fenti feltételezés elfogadása esetén a \(\displaystyle G\) nagyságú, függőleges irányú nehézségi erő, a lejtő síkjára merőleges \(\displaystyle N\) nagyságú nyomóerő, a lejtő esésvonala mentén (felfelé) ható \(\displaystyle S\) súrlódási erő és a megmozdításhoz szükséges \(\displaystyle F\) nagyságú erő mind ugyanabban a síkban lévő vektorok, a feladat tehát síkbeli problémaként kezelhető (1. ábra).
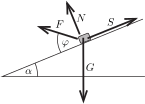
1. ábra
Vizsgáljuk azt a helyzetet, amelyben a test még éppen nem csúszik meg, még egyensúlyban van. Az erőegyensúly feltétele:
| \(\displaystyle (1)\) | \(\displaystyle N=G\cos\alpha-F\sin\varphi,\) |
| \(\displaystyle (2)\) | \(\displaystyle S=G\sin\alpha+F\cos\varphi,\) |
és a megcsúszás határhelyzetében
| \(\displaystyle (3)\) | \(\displaystyle S=\mu N.\) |
A (1) és (2) egyenletek jobb oldalát (3)-ba helyettesítve, majd abból \(\displaystyle F\)-et kifejezve kapjuk, hogy \(\displaystyle F\) mint \(\displaystyle \varphi\) függvénye:
| \(\displaystyle (4)\) | \(\displaystyle F(\varphi)=\frac{\mu\cos\alpha-\sin\alpha}{\cos\varphi+\mu \sin\varphi}\,G.\) |
A számlálóban lévő kifejezés pozitív (hiszen a test ,,magától'' nem csúszik le a lejtőn, tehát \(\displaystyle \mu>\tg\alpha\)). Ennek megfelelően \(\displaystyle F\) akkor a legkisebb, amikor a nevező a legnagyobb értéket veszi fel.
A maximum helyét háromféle módszerrel is meg lehet határozni:
a) Differenciálszámítással.
\(\displaystyle \frac{\mathrm{d}}{\mathrm{d}\varphi}(\cos\varphi+\mu\sin\varphi)=-\sin\varphi+\mu\cos\varphi=0,\)
vagyis \(\displaystyle \tg\varphi=\mu\), és a maximum nagysága
\(\displaystyle \frac{1}{\sqrt{1+\mu^2}}+\mu\frac{\mu}{\sqrt{1+\mu^2}}=\sqrt{1+\mu^2}.\)
b) Geometriai megfontolással. Ha egy \(\displaystyle \mu\) és \(\displaystyle 1\) oldalélű téglalapot függőleges helyzetben vízszintes síklapra állítunk, majd az egyik csúcsa körül a saját síkjában \(\displaystyle \varphi\) szöggel elforgatjuk, az átlósan szemközti csúcsa éppen olyan magasra kerül, mint (4) nevezője (2. ábra). Ez a magasság akkor a legnagyobb, amikor a kérdéses átló éppen függőleges, vagyis \(\displaystyle \tg\varphi=\mu,\) és a maximális érték az átló hossza, vagyis\(\displaystyle \sqrt{1+\mu^2}.\)
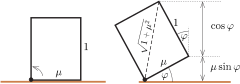
2. ábra
Ezek szerint (4) jobb oldalának legkisebb értéke
\(\displaystyle F_0=\left(\frac{\mu\cos\alpha}{\sqrt{1+\mu^2}}-\frac{\sin\alpha}{\sqrt{1+\mu^2}}\right)G.\)
A test tehát akkor mozdítható meg a lejtőn a legkönnyebben, ha \(\displaystyle F_0\)-nál bármilyen kicsivel nagyobb erőt fejtünk ki rá a lejtő esésvonalának lefelé tartó részével \(\displaystyle \arctg\mu\) szöget bezáró irányban, ferdén felfelé.
c) Trigonometriai átalakításokkal. A súrlódási együtthatót sok esetben érdemes felírni \(\displaystyle \mu=\tg\varepsilon\) alakban, ahol \(\displaystyle \varepsilon=\arctg\mu\) az ún. súrlódási határszög. Mivel a test külső erőhatás nélkül nem csúszik le a lejtőn, fennáll \(\displaystyle \mu>\tg\alpha\), azaz \(\displaystyle \varepsilon>\alpha\). Ezzel a jelöléssel (4) ilyen alakot ölt:
\(\displaystyle F(\varphi)=\frac{\tg\varepsilon\cos\alpha-\sin\alpha}{\cos\varphi+\tg\varepsilon\sin\varphi}G=\frac{\sin\varepsilon\cos\alpha-\cos\varepsilon\sin\alpha}{\cos\varepsilon\cos\varphi+\sin\varepsilon\sin\varphi}\,G=\frac{\sin(\varepsilon-\alpha)}{\cos(\varepsilon-\varphi)}\,G.\)
Ennek minimuma a nevező maximumánál, vagyis \(\displaystyle \varphi=\varepsilon\), azaz \(\displaystyle \tg\varphi=\mu\) értéknél van, és a maximum nagysága
\(\displaystyle F_0=\sin(\varepsilon-\alpha)\,G=(\sin\varepsilon\cos\alpha-\cos\varepsilon\sin\alpha)\,G=\left(\frac{\mu\cos\alpha}{\sqrt{1+\mu^2}}-\frac{\sin\alpha}{\sqrt{1+\mu^2}}\right)G.\)
II. megoldás. Ebben a megoldásban nem élünk azzal a feltevéssel, hogy a testre ható valamennyi erő ugyanabban a síkban helyezkedik el, hanem megengedjük, hogy az \(\displaystyle \boldsymbol{S}\) súrlódási erőnek és az általunk kifejtett \(\displaystyle \boldsymbol{F}\) erőnek legyen a lejtő szintvonalaival párhuzamos komponense is. A 3. ábrán látható térbeli koordináta-rendszert fogjuk használni, amelyben az \(\displaystyle x\) tengely a lejtő szintvonalaival párhuzamos, az \(\displaystyle y\) tengely az esésvonal irányába mutat, a \(\displaystyle z\) tengely pedig merőleges a jeltő síkjára.
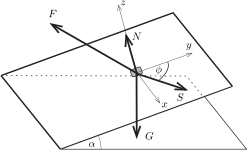
3. ábra
A lejtő által kifejtett nyomóerő vektora
\(\displaystyle \boldsymbol{N}=(0,0,N),\)
a nehézségi erő
\(\displaystyle \boldsymbol{G}=(0,-G\sin\alpha,-G\cos\alpha).\)
A súrlódási erő az \(\displaystyle (x,y)\) síkban fekszik, a nagysága a megcsúszás határhelyzetében \(\displaystyle S=\mu N\), és \(\displaystyle \boldsymbol{S}\) irányának az \(\displaystyle y\) tengellyel bezárt szögét jelöljük \(\displaystyle \phi\)-vel; így a komponensei:
\(\displaystyle \boldsymbol{S}=(\mu N\sin\phi,\mu N\cos\phi,0).\)
Az \(\displaystyle \boldsymbol{N}\) vektor nagyságát érdemes \(\displaystyle N=\xi G\) alakban felírni, ahol \(\displaystyle \xi\) egy dimenziótlan mennyiség.
Erőegyensúly esetén
\(\displaystyle \boldsymbol{N}+\boldsymbol{G}+\boldsymbol{S}+\boldsymbol{F}=0,\)
vagyis
\(\displaystyle \boldsymbol{F}=G\left(-\mu\xi\sin\phi,\,\sin\alpha-\mu\xi\cos\phi,\,\cos\alpha-\xi\right),\)
ahonnan a minimalizálandó kétváltozós függvény
| \(\displaystyle (5))\) | \(\displaystyle f(\xi,\phi)\equiv\frac{F^2}{G^2}=\xi^2(1+\mu^2)-2\xi(\mu\sin\alpha\cos\phi+\cos\alpha)+1.\) |
(Kihasználtuk, hogy \(\displaystyle F\) legkisebb értékénél \(\displaystyle F^2/G^2\) is minimális.)
A \(\displaystyle \phi\) változó (5)-ben csak egyetlen tagban szerepel, nevezetesen a \(\displaystyle -\cos\phi\) kifejezésnek pozitív számszorosaként. Ennek bármilyen \(\displaystyle \xi\) mellett \(\displaystyle \phi=0\)-nál a legkisebb az értéke.
Megjegyzés. Ezzel bizonyítást nyert az I. megoldásban megfogalmazott sejtés, vagyis az, hogy a feladat síkbeli problémaként kezelhető.
A továbbiakban az
| \(\displaystyle (6)\) | \(\displaystyle f(\xi,\phi=0)\equiv\xi^2(1+\mu^2)-2\xi(\mu\sin\alpha +\cos\alpha)+1\) |
egyváltozós, a \(\displaystyle \xi\) változóban másodfokú függvény legkisebb értékét keressük meg. (6) jobb oldala teljes négyzetté alakítható, és abból könnyen leolvashatjuk a minimum helyét és nagyságát:
\(\displaystyle \frac{F^2}{G^2}=\left(\xi\sqrt{1+\mu^2}-\frac{\mu\sin\alpha+\cos\alpha }{\sqrt{1+\mu^2}}\right)^2+1-\frac{(\mu\sin\alpha+\cos\alpha)^2}{1+\mu^2}\ge 1-\frac{(\mu\sin\alpha+\cos\alpha)^2}{1+\mu^2}=\left(\frac{\mu\cos\alpha-\sin\alpha }{\sqrt{1+\mu^2}}\right)^2.\)
Ezek szerint a test megmozdításához szükséges erő nagyságának alsó határa (\(\displaystyle F=F_0\) esetén a test még egyensúlyban marad, de \(\displaystyle F_0\)-at bármilyen kicsiny mértékben meghaladó nagyságú és alkalmasan választott irányba mutató erővel már megmozdítható):
\(\displaystyle F_0=\frac{\mu\cos\alpha-\sin\alpha }{\sqrt{1+\mu^2}}\,G.\)
III. megoldás. A II. megoldás jelöléseit használva az egyensúly \(\displaystyle \vert\boldsymbol{S}\vert\le\mu\vert\boldsymbol{N}\vert\) feltétele úgy is megfogalmazható, hogy a test mindaddig mozdulatlan marad, ameddig a test helyétől felmérve a lejtő által kifejtett teljes kényszererő \(\displaystyle \boldsymbol{K}=\boldsymbol{N}+\boldsymbol{S}\) vektorának végpontja egy olyan körkúp belsejébe vagy annak palástjára esik, amelynek szimmetriatengelye merőleges a lejtő síkjára, és a félnyílásszöge a súrlódás \(\displaystyle \varepsilon=\arctg\mu\) határszöge (4. ábra).
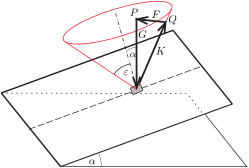
4. ábra
A testre ható erők egyensúlyi állapotban zárt vektorháromszöget alkotnak. A \(\displaystyle \boldsymbol{G}\) nehézségi erő függőleges, hatásvonala \(\displaystyle \alpha\) szöget zár be a kúp szimmetriatengelyével. A \(\displaystyle \boldsymbol{K}\) kényszererő a megcsúszás határesetében a kúp palástjának valamelyik \(\displaystyle Q\) pontjába mutat. Végül az egyensúlyt biztosító \(\displaystyle \boldsymbol{F}\) külső erő a \(\displaystyle Q\) pontot a nehézségi erő vektorának \(\displaystyle P\) kezdőpontjával köti össze.
Feladatunk a kúppalást azon \(\displaystyle Q\) pontjának megtalálása, amelyre a \(\displaystyle PQ\) távolság a legkisebb. Tekintsük a \(\displaystyle P\) középpontú, \(\displaystyle F\) sugarú gömbfelületeket. Ha \(\displaystyle F\) túlságosan kicsi, a gömb teljes egészében a kúp belsejébe esik, tehát a test nem mozdul meg. Növelve \(\displaystyle F\) nagyságát, valamekkora \(\displaystyle F_0\) sugárnál a gömb felülete valahol eléri a kúp palástját, a két felület egy \(\displaystyle Q\) pontban érinti egymást. Ennél a pontnál a kúp palástjának érintősíkja egybeesik a gömb érintősíkjával, tehát merőleges az \(\displaystyle \boldsymbol{F}\) vektorra. Ez csak akkor akkor teljesülhet, ha a \(\displaystyle Q\) pont illeszkedik a lejtő esésvonalán átmenő függőleges síkra.
Megjegyzés. Ez az észrevétel is bizonyítja az I. megoldásban szereplő sejtés helyességét, vagyis azt, hogy a feladat síkbeli problémaként kezelhető.
(Kivételt képez az \(\displaystyle \alpha=0\) eset, amikor a test nem lejtőn, hanem egy vízszintes felületen nyugszik. Ilyenkor a gömb nem egyetlen pontban, hanem egy vízszintes kör mentén érinti a kúppalástot.)
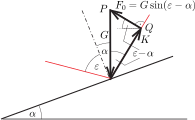
5. ábra
A \(\displaystyle PQ\) távolság legkisebb értékét könnyen leolvashatjuk az 5. ábráról, ami a kúp palástjának az esésvonalra és a szimmetriatengelyre illeszkedő síkmetszetét mutatja. \(\displaystyle F=PQ\) akkor a legkisebb, ha \(\displaystyle \boldsymbol{F}\) merőleges \(\displaystyle \boldsymbol{K}\)-ra, és ekkor az általunk kifejtett erő nagysága
\(\displaystyle F_0=G\sin(\varepsilon-\alpha)=G(\sin\varepsilon\cos\alpha-\cos\varepsilon\sin\alpha)=\left(\frac{\mu\cos\alpha}{\sqrt{1+\mu^2}}-\frac{\sin\alpha}{\sqrt{1+\mu^2}}\right)G.\)
Az is látszik az 5. ábrán, hogy \(\displaystyle \boldsymbol{F}_0\) a vízszintessel \(\displaystyle \varepsilon-\alpha\) szöget, a lejtő síkjával pedig éppen \(\displaystyle \varepsilon\) nagyságú szöget zár be. \(\displaystyle F=F_0\) nagyságú külső erőnél a test még éppen egyensúlyban van, de ha \(\displaystyle F\) tetszőlegesen kicsiny értékkel meghaladja \(\displaystyle F_0\)-t, a gömb egy kicsiny része a kúpon kívülre kerül, tehát ekkor a tapadó súrlódás nem tudja megakadályozni a test megmozdulását.
Statisztika:
54 dolgozat érkezett. 5 pontot kapott: Bense Tamás, Blaskovics Ádám, Bús László Teodor, Csáti Ambrus, Erdélyi Dominik, Halmosi Dávid, Hornyák Zalán Zétény, Horváth Péter, Kávrán-Kőnig Balázs, Kossár Benedek Balázs, Kovács Tamás , Lakatos Levente, Magyar Levente Árpád, Mezei Marcell, Mi Feiyu, Molnár Lili, Nagy Gellért Ákos, Nyitrai Csenger, Patócs 420 Péter, Rajtik Sándor Barnabás, Simon János Dániel, Sipeki Andor, Szabó Tamás, Szécsi Bence, Tasnádi Zsófia, Tóth Hanga Katalin, Török Tibor, Vértesi Janka, Vigh István Csaba, Winhoffer Júlia, Zádori Gellért, Zhao Aaron . 4 pontot kapott: Gilyán Zsombor, Hornok Máté, Horváth Zsombor, Kádár Luca Linda, Papp Emese Petra, Sümeghi Nándor , Wolf Erik. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 3 versenyző.
A KöMaL 2025. decemberi fizika feladatai

