 |
A P. 5691. feladat (2025. december) |
P. 5691. Határozzuk meg egy vékony, \(\displaystyle m\) tömegű, homogén tömegeloszlású, \(\displaystyle a\) oldalú szabályos háromszög alakú lemez tehetetlenségi nyomatékát az egyik csúcsán áthaladó tengelyre vonatkozóan, ha az
a) a háromszög síkjára merőleges,
b) a magasságvonal,
c) az előző két tengelyre merőleges.
Közli: Zsigri Ferenc, Budapest
(5 pont)
A beküldési határidő 2026. január 15-én LEJÁRT.
I. megoldás. a) Határozzuk meg először a \(\displaystyle \Theta_\mathrm{a,\,tkp}\) tehetetlenségi nyomatékot a háromszög tömegközéppontján átmenő (és a háromszög síkjára merőleges) tengelyre. Ehhez osszuk fel a szabályos háromszöget 4 egybevágó kis háromszögre, ahogy azt az 1. ábra mutatja.
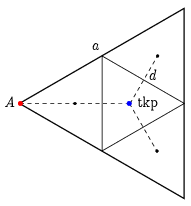
1. ábra
Egy kis háromszög saját tömegközéppontján átmenő tengelyre vonatkozó tehetetlenségi nyomatéka a nagy háromszögének 1/16-od része, hiszen a kis lemez tömege a nagy tömegének negyede, a lineáris méretei pedig a nagy méreteinek fele, de ezek a tehetetlenségi nyomatékban négyzetesen szerepelnek. Rakjuk össze a nagy háromszög tehetetlenségi nyomatékát a négy kis háromszögéből a Steiner-tétel segítségével:
\(\displaystyle \Theta_\mathrm{a,\,tkp}=4\frac{\Theta_\mathrm{a,\,tkp}}{16}+3\frac{m}{4}d^2,\)
ahol \(\displaystyle d=\tfrac{a}{2\sqrt{3}}\) a három nem középen lévő kis háromszög tömegközéppontjának távolsága a közös tömegközépponttól. Ezt behelyettesítve és rendezve:
\(\displaystyle \Theta_\mathrm{a,\,tkp}=\frac{1}{12}ma^2.\)
Ebből a keresett tehetetlenségi nyomaték a Steiner-tétel alapján (felhasználva, hogy a tömegközéppont és a csúcs távolsága \(\displaystyle \tfrac{a}{\sqrt{3}}\)):
\(\displaystyle \Theta_\mathrm{a}=\Theta_\mathrm{a,\,tkp}+m\frac{a^2}{3}=\frac{5}{12}ma^2.\)
b) Hasonló módszerrel dolgozhatunk a \(\displaystyle \Theta_\mathrm{b}\) tehetetlenségi nyomaték meghatározásakor is: a 2. ábrán látható módon ugyanúgy 4 kis háromszögre bontjuk a nagy háromszöget.
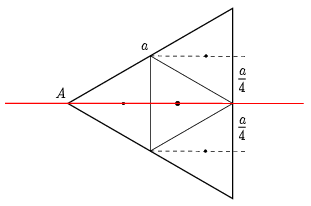
2. ábra
A kis háromszögek magasságvonalra vonatkoztatott tehetetlenségi nyomatéka az előzőhöz hasonlóan a nagy háromszög magasságvonalra vonatkozó tehetetlenségi nyomatékának 1/16-od része. A nagy háromszög tehetetlenségi nyomatékát ismét a négy kis háromszögéből rakjuk össze a Steiner-tétel segítségével:
\(\displaystyle \Theta_\mathrm{b}=4\frac{\Theta_\mathrm{b}}{16}+2\frac{m}{4}\frac{a^2}{16},\)
ahol felhasználtuk, hogy most csak két kis háromszög tömegközéppontja nem esik a tengelyre, és ezek tömegközéppontja \(\displaystyle \tfrac{a}{4}\) távolságra van a tengelytől. Ebből rendezve a keresett tehetetlenségi nyomaték:
\(\displaystyle \Theta_\mathrm{b}=\frac{1}{24}ma^2.\)
c) Most az a) részhez hasonlóan először a tömegközépponton átmenő, az egyik oldallal párhuzamos \(\displaystyle \Theta_\mathrm{c,\,tkp}\) tehetetlenségi nyomatékot határozzuk meg ugyanezzel a módszerrel (3. ábra).
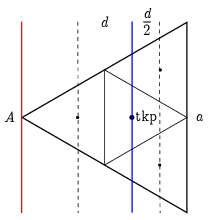
3. ábra
Egy kis háromszög tömegközépponton átmenő, egyik oldallal párhuzamos tengelyre vonatkozó tehetetlenségi nyomatéka az előzőkhöz hasonlóan most is a nagy háromszög tehetetlenségi nyomatékának 1/16-od része. A nagy háromszög tehetetlenségi nyomatékát ismét a négy kis háromszögéből rakjuk össze a Steiner-tétel segítségével:
\(\displaystyle \Theta_\mathrm{c,\,tkp}=4\frac{\Theta_\mathrm{c,\,tkp}}{16}+2\frac{m}{4}\frac{d^2}{4}+\frac{m}{4}d^2,\)
ahol ismét \(\displaystyle d=\tfrac{a}{2\sqrt{3}}\), és felhasználtuk, hogy két kis háromszög tömegközéppontja \(\displaystyle \tfrac{d}{2}\), egy pedig \(\displaystyle d\) távolságra van a nagy háromszög tömegközéppontján átmenő tengelytől. Ezt behelyettesítve és rendezve:
\(\displaystyle \Theta_\mathrm{c,\,tkp}=\frac{1}{24}ma^2.\)
Ebből a keresett tehetetlenségi nyomaték a Steiner-tétel alapján (ismét felhasználva, hogy a tömegközéppont és a csúcs távolsága \(\displaystyle \tfrac{a}{\sqrt{3}}\)):
\(\displaystyle \Theta_\mathrm{c}=\Theta_\mathrm{c,\,tkp}+m\frac{a^2}{3}=\frac{3}{8}ma^2.\)
Megjegyzések. 1. Vegyük észre, hogy \(\displaystyle \Theta_\mathrm{a}=\Theta_\mathrm{b}+\Theta_\mathrm{c}\) (\(\displaystyle \tfrac{5}{12}=\tfrac{1}{24}+\tfrac{3}{8}\)). Ez nem véletlen! Egy síkidom tehetetlenségi nyomatéka bármely tengelyre a \(\displaystyle \Theta=\sum m_id_i^2\) összefüggéssel számítható ki, ahol \(\displaystyle d_i\) az adott kis tömegelem távolsága a kiválasztott tengelytől. A 4. ábrán látható, hogy a síklapra merőleges \(\displaystyle a\) tengelytől mért \(\displaystyle d_{a,\,i}\) távolságra fennáll, hogy \(\displaystyle d_{a,\,i}^2=d_{b,\,i}^2+d_{c,\,i}^2\), ahol \(\displaystyle d_{b,\,i}\) és \(\displaystyle d_{c,\,i}\) a síkban lévő, egymásra merőleges \(\displaystyle b\) és \(\displaystyle c\) tengelyektől mért távolságok.
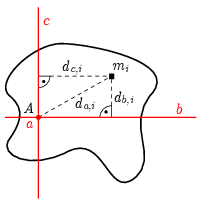
4. ábra
Ebből és a tehetetlenségi nyomaték fenti összegzős képletéből azonnal adódik az összefüggés. (Ennek ismeretében a három feladatrész egyikének kiszámítása megspórolható lehet.)
2. A megoldáshoz más feldarabolással is el lehet jutni.
II. megoldás. A tehetetlenségi nyomatékok kiszámíthatók integrálszámítással is. Itt most a háromszöglapot \(\displaystyle \mathrm{d}x\) szélességű, \(\displaystyle \ell=\tfrac{2}{\sqrt{3}}x\) hosszúságú kis téglalapokból fogjuk összerakni (5. ábra), amelyek tehetetlenségi nyomatéka a középpontjukon átmenő, a szakaszra merőleges tengelyekre \(\displaystyle \mathrm{d}\Theta=\tfrac{1}{12}\ell^2\mathrm{d}m\), a szakaszon átmenő tengelyre pedig nulla. A kis szakasz tömegét a \(\displaystyle \mathrm{d}m=\tfrac{m}{A}\ell\mathrm{d}x\) összefüggéssel fejezhetjük ki, ahol \(\displaystyle A=\tfrac{\sqrt{3}}{4}a^2\) a háromszög területe. Ahol szükséges, használjuk a Steiner-tételt.
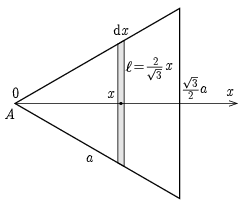
5. ábra
a)
\(\displaystyle \Theta_\mathrm{a}=\int\limits_0^{\frac{\sqrt{3}}{2}a}\left(x^2+\frac{1}{12}\ell^2\right)\frac{4m}{\sqrt{3}a^2}\ell\mathrm{d}x=\frac{80m}{27a^2}\int\limits_0^{\frac{\sqrt{3}}{2}a}x^3\mathrm{d}x=\frac{80m}{27a^2}\left[\frac{1}{4}x^4\right]_0^{\frac{\sqrt{3}}{2}a}=\frac{5}{12}ma^2.\)
b)
\(\displaystyle \Theta_\mathrm{b}=\int\limits_0^{\frac{\sqrt{3}}{2}a}\frac{1}{12}\ell^2\frac{4m}{\sqrt{3}a^2}\ell\mathrm{d}x=\frac{8m}{27a^2}\int\limits_0^{\frac{\sqrt{3}}{2}a}x^3\mathrm{d}x=\frac{8m}{27a^2}\left[\frac{1}{4}x^4\right]_0^{\frac{\sqrt{3}}{2}a}=\frac{1}{24}ma^2.\)
c)
\(\displaystyle \Theta_\mathrm{a}=\int\limits_0^{\frac{\sqrt{3}}{2}a}x^2\frac{4m}{\sqrt{3}a^2}\ell\mathrm{d}x=\frac{8m}{3a^2}\int\limits_0^{\frac{\sqrt{3}}{2}a}x^3\mathrm{d}x=\frac{8m}{3a^2}\left[\frac{1}{4}x^4\right]_0^{\frac{\sqrt{3}}{2}a}=\frac{3}{8}ma^2.\)
Megjegyzések. 1. Már az integrálás elvégzése előtt látszik, hogy teljesül a \(\displaystyle \Theta_\mathrm{a}=\Theta_\mathrm{b}+\Theta_\mathrm{c}\) összefüggés.
2. Az integrálás más felosztással is elvégezhető.
Statisztika:
30 dolgozat érkezett. 5 pontot kapott: Bogdán Balázs Ákos, Erdélyi Dominik, Horváth Péter, Horváth Zsombor, Kávrán-Kőnig Balázs, Kossár Benedek Balázs, Kovács Tamás, Mezei Marcell, Nyitrai Csenger, Papp Emese Petra, Patócs 420 Péter, Rajtik Sándor Barnabás, Simon János Dániel, Szabó Tamás, Szécsi Bence, Tajta Sára, Tasnádi Zsófia, Török Tibor, Vincze Anna, Zádori Gellért. 4 pontot kapott: Sümeghi Nándor , Zólomy Csanád Zsolt. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 3 versenyző.
A KöMaL 2025. decemberi fizika feladatai

