 |
A P. 5692. feladat (2025. december) |
P. 5692. Egy adott mennyiségű egyatomos ideális gáz kvázisztatikusan eljut a kezdeti \(\displaystyle p_0\) nyomású és \(\displaystyle V_0\) térfogatú állapotából a \(\displaystyle p_0\) nyomású és \(\displaystyle 2V_0\) térfogatú végállapotába. A folyamatot úgy választjuk meg, hogy a gáz hőmérséklete sohasem csökkenhet, illetve a gáz sohasem adhat le hőt.
a) Minimálisan mekkora hőt közölhettünk a gázzal?
b) Maximálisan mekkora hőt közölhettünk a gázzal?
KVANT feladat
(5 pont)
A beküldési határidő 2026. január 15-én LEJÁRT.
I. megoldás. A \(\displaystyle pV\) állapotsíkon azok a folyamatok, amelyek során a hőmérséklet nem változik, a \(\displaystyle pV=\textrm{állandó}\) izotermákkal, azok a folyamatok pedig, ahol nincs hőfelvétel vagy leadás, a \(\displaystyle pV^\kappa=\textrm{állandó}\) adiabatákkal ábrázolhatók. Esetünkben a \(\displaystyle \kappa=c_p/c_V\) fajhőhányados – egyatomos gázról lévén szó – 5/3. Azoknak a folyamatoknak a \(\displaystyle p(V)\) függvénye, amelyeknél nincs hőleadás, és a hőmérséklet nem csökkenhet, az adiabatákat és az izotermákat csak a megfelelő oldalról metszhetik. Ez minden pontban kijelöli a megengedett irányokat. Ábrázoljuk a \(\displaystyle p_0\) és \(\displaystyle V_0\) értékekkel jellemzett A kezdő-, és a \(\displaystyle p_0\), \(\displaystyle 2V_0\) értékekkel megadott B végponton átmenő adiabatákat és izotermákat. Jelöljük az A-n átmenő \(\displaystyle pV=p_0V_0\) izoterma és a B-vel meghatározott \(\displaystyle pV^{\kappa}=p_0(2V_0)^{\kappa}\) adiabata metszéspontját K\(\displaystyle _1\)-gyel, a B-n átmenő \(\displaystyle pV=p_0(2V_0)\) izoterma és az A-t tartalmazó \(\displaystyle pV^{\kappa}=p_0V_0^{\kappa}\) adiabata metszéspontját pedig K\(\displaystyle _2\)-vel. Könnyen belátható, hogy azokon az utakon, amik az A-K\(\displaystyle _2\) és K\(\displaystyle _1\)-B adiabaták valamint a K\(\displaystyle _2\)-B és A-K\(\displaystyle _1\) izotermák jelentette keretből kilépnek, a feltételeink valahol sérülnek, tehát a szóba jöhető folyamatok ezen görbék által meghatározott terület belsejében, vagy a határain kell, hogy végbemenjenek. (Az állítás megfordítva nem igaz, nem minden folyamat, amely az AK\(\displaystyle _2\)BK\(\displaystyle _1\) idom belsejében ábrázolható, felel meg a hőmérséklet-csökkenés és hőleadás tilalmának.) A helyzetet vázlatosan mutató 1. ábrán megrajzoltuk a határokon futó A\(\displaystyle \to\)K\(\displaystyle _1\!\to\)B, valamint A\(\displaystyle \to\)K\(\displaystyle _2\!\to\)B folyamatokat, és bejelöltünk egy lehetséges közvetlen A\(\displaystyle \to\)B utat is.
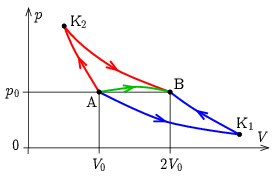
1. ábra
Az alábbiakban megmutatjuk, hogy az egyes folyamatokhoz tartozó \(\displaystyle Q_\mathrm{AK_1B}\), \(\displaystyle Q_\mathrm{AK_2B}\) és \(\displaystyle Q_\mathrm{AB}\) hőfelvételekre igaz a
\(\displaystyle Q_\mathrm{AK_2B}>Q_\mathrm{AB}>Q_\mathrm{AK_1B}\)
reláció. Tekintsük az A\(\displaystyle \to\)K\(\displaystyle _2\!\to\)B\(\displaystyle \to\)A körfolyamatot, ahol rendszer az A-ból B-be a határon futó A\(\displaystyle \to\)K\(\displaystyle _2\!\to\)B úton jut el, vissza pedig a bejelölt közvetlen A-B görbe mentén a jelölttel ellentétes irányba haladva. A körfolyamat során a hőfelvétel \(\displaystyle Q_\mathrm{AK_2B}\), a hőleadás pedig \(\displaystyle Q_\mathrm{AB}\), a kettő \(\displaystyle W=Q_\mathrm{AK_2B}-Q_\mathrm{AB}\) különbsége pedig a végzett munka. Ez az adott körbejárási irány mellett pozitív, tehát valóban
\(\displaystyle Q_\mathrm{AK_2B}>Q_\mathrm{AB}.\)
Teljesen analóg módon az A\(\displaystyle \to\)B\(\displaystyle \to\)K\(\displaystyle _1\!\to\)A körfolyamatot tekintve megkapjuk a
\(\displaystyle Q_\mathrm{AB}>Q_\mathrm{AK_1B}\)
relációt is. Mivel az A\(\displaystyle \to\)B egy tetszőleges, a kijelölt tartomány belsejében végbevitt, a feltételeket kielégítő folyamat, a lehetséges legnagyobb és legkisebb hőfelvétel a határokon futó A\(\displaystyle \to\)K\(\displaystyle _2\!\to\)B, illetve A\(\displaystyle \to\)K\(\displaystyle _1\!\to\)B úton van:
\(\displaystyle Q_\mathrm{max}=Q_\mathrm{AK_2B},\qquad Q_\mathrm{min}=Q_\mathrm{AK_1B}.\)
Az A\(\displaystyle \to\)K\(\displaystyle _2\!\to\)B folyamat során hőfelvétel csak az izotermikus K\(\displaystyle _2\!\to\)B szakaszon van. Mivel itt a rendszer belső energiája nem változik, a felvett hő azonos a rendszer tágulási munkájával, azaz
\(\displaystyle Q_\mathrm{max}=\sum\Delta Q=\sum_\mathrm{K_2\to B}p\Delta V.\)
Az adott izoterma egyenlete szerint
\(\displaystyle p=\frac{p_02V_0}{V},\)
így
\(\displaystyle Q_\mathrm{max}=2p_0V_0\sum_\mathrm{K_2\to B}\frac{\Delta V}{V}.\)
A \(\displaystyle \Delta V\) lépéseket egyre kisebbre választva az összefüggésünk jobb oldalán az összeg a megfelelő integrál értékéhez közelít,
\(\displaystyle \sum_\mathrm{K_2\to B}\frac{\Delta V}{V}\to\int\limits_{V_\mathrm{K_2}}^{V_\mathrm{B}}\frac{\mathrm{d}V}{V},\)
ami a Függvénytáblázatok szerint
\(\displaystyle \int\limits_{V_\mathrm{K_2}}^{V_\mathrm{B}}\frac{\mathrm{d}V}{V}=\ln\frac{V_\mathrm{B}}{V_\mathrm{K_2}}.\)
Definíciónk szerint K\(\displaystyle _2\) a \(\displaystyle pV=p_0(2V_0)\) izoterma és a \(\displaystyle pV^\kappa=p_0V_0^\kappa\) adiabata metszéspontja, ahol is
\(\displaystyle V_\mathrm{K_2}^{\kappa-1}=\frac{V_{0}^{\kappa-1}}{2},\qquad\textrm{azaz}\qquad V_\mathrm{K_2}=\frac{V_0}{2^{1/(\kappa-1)}}.\)
Mivel \(\displaystyle V_\mathrm{B}=2V_0\),
\(\displaystyle \frac{V_\mathrm{B}}{V_\mathrm{K_2}}=2^{\kappa/(\kappa-1)},\)
tehát
\(\displaystyle Q_\mathrm{max}=2p_0V_0\ln{2^{\kappa/(\kappa-1)}}=p_0V_0\frac{2\kappa\ln 2}{\kappa-1}=5p_0V_0\ln 2.\)
Teljesen hasonló módon ki tudjuk számolni az A\(\displaystyle \to\)K\(\displaystyle _1\) úton felvett \(\displaystyle Q_\mathrm{min}\) értékét, de van ennél egy rövidebb út is. Vegyük észre, hogy az A\(\displaystyle \to\)K\(\displaystyle _2\!\to\)B\(\displaystyle \to\)K\(\displaystyle _1\!\to\)A folyamat egy Carnot-körfolyamat, aminek a felső hőtartálya az állapotegyenlet szerint kétszer akkora hőmérsékletű, mint az alsó (\(\displaystyle T_\mathrm{B}=2p_0V_0/nR\), illetve \(\displaystyle T_\mathrm{A}=p_0V_0/nR\)), tehát a hatásfoka \(\displaystyle \eta=1/2\). Ennek megfelelően
\(\displaystyle \eta =\frac{Q_\mathrm{max}-Q_\mathrm{min}}{Q_\mathrm{max}}=\frac{1}{2},\)
amiből
\(\displaystyle Q_\mathrm{min}=\frac{Q_\mathrm{max}}{2}=\frac{5}{2}p_0V_0\ln 2.\)
Megjegyzés. Carnot tétele szerint bármely két hőmérséklet között végbevihető körfolyamatok közül a Carnot-körfolyamatnak a legjobb a hatásfoka. Ebből kiindulva is könnyen igazolható a \(\displaystyle Q_\mathrm{max}=Q_\mathrm{AK_2B}\) és \(\displaystyle Q_\mathrm{min}=Q_\mathrm{AK_1B}\) állításokat megalapozó \(\displaystyle Q_\mathrm{AK_2B}>Q_\mathrm{AB}>Q_\mathrm{AK_1B}\) reláció. Innen tekintve a dolgot a fenti gondolatmenetünk a Carnot-tétel igazolásának tekinthető a lehetséges folyamatok egy osztályára (nevezetesen azokra, ahol a hőfelvétel és hőmérséklet-emelkedés, illetve a hőleadás és a hőmérséklet-csökkenés egy-egy szakaszban történik).
II. megoldás. Legyen a gáz hőmérséklete kezdetben \(\displaystyle T_\mathrm{A}=T_0\), ekkor az ideális gáz \(\displaystyle pV=nRT\) állapotegyenlete alapján a végállapotban \(\displaystyle T_\mathrm{B}=2T_0\). Ábrázoljuk a kezdeti és a végállapotot, valamint a lehetséges folyamatokat az \(\displaystyle T\)-\(\displaystyle S\) állapotsíkon (2. ábra). Az entrópia kezdeti értékét nem tudjuk meghatározni (nincs is rá szükségünk), csak a megváltozását:
\(\displaystyle \Delta S=\frac{3}{2}nR\ln\frac{T_\mathrm{B}}{T_\mathrm{A}}+nR\ln\frac{V_\mathrm{B}}{V_\mathrm{A}}=\frac{5\ln 2}{2}nR=\frac{5\ln 2}{2}\frac{p_0V_0}{T_0},\)
ahol felhasználtuk, hogy \(\displaystyle \tfrac{T_\mathrm{B}}{T_\mathrm{A}}=\tfrac{V_\mathrm{B}}{V_\mathrm{A}}=2\), az egyatomos gáznál \(\displaystyle f=3\), valamint az állapotegyenlet alapján az \(\displaystyle nR=\tfrac{p_0V_0}{T_0}\) összefüggést.
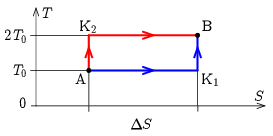
2. ábra
Ha a gáz hőmérséklete sohasem csökkenhet, illetve a gáz sohasem adhat le hőt, akkor se \(\displaystyle T\), se \(\displaystyle S\) nem csökkenhet, az A állapotból a B állapotba az \(\displaystyle S\)-\(\displaystyle T\) állapotsíkon csak egy egyértékű, monoton növekvő görbe mentén juthat el a gáz. A gáz által felvett hőt az \(\displaystyle S\)-\(\displaystyle T\) állapotsíkon a görbe alatti terület adja meg (hiszen \(\displaystyle \mathrm{d}Q=T\mathrm{d}S\)), így a minimális hőközléshez az A-K\(\displaystyle _1\)-B egyenes szakaszokból álló útvonal, a maximális hőközléshez az A-K\(\displaystyle _2\)-B útvonal tartozik. (\(\displaystyle T\) és \(\displaystyle S\) értéke nem csökkenhet, de lehet állandó.) Ez alapján a keresett minimális és maximális hőközlés:
a)
\(\displaystyle Q_\mathrm{min}=T_0\Delta S=\frac{5\ln 2}{2}p_0V_0=1{,}73\,p_0V_0,\)
b)
\(\displaystyle Q_\mathrm{max}=2T_0\Delta S=5\ln 2\,p_0V_0=3{,}46\,p_0V_0=2Q_\mathrm{min}.\)
Statisztika:
31 dolgozat érkezett. 5 pontot kapott: Békési Máté, Erdélyi Dominik, Fuchs Vince, Kossár Benedek Balázs, Patócs 420 Péter, Rajtik Sándor Barnabás, Zólomy Csanád Zsolt. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 15 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2025. decemberi fizika feladatai

