 |
A P. 5693. feladat (2025. december) |
P. 5693. Hat darab egyforma \(\displaystyle R\) ellenállásból egy \(\displaystyle ABCD\) tetraédert állítunk össze, és a tetraéder \(\displaystyle A\) és \(\displaystyle B\), valamint \(\displaystyle C\) és \(\displaystyle D\) csúcsa közé egy-egy \(\displaystyle U_0\) feszültségű telepet kapcsolunk. Mennyi hő fejlődik adott \(\displaystyle T\) idő alatt az egész hálózaton? (A telepek belső ellenállása elhanyagolható.)
Példatári feladat nyomán
(4 pont)
A beküldési határidő 2026. január 15-én LEJÁRT.
I. megoldás. Az 1. ábrán a feladatban leírt hálózat látható felülnézetből. A tetraéder minden pontja egyforma ellenállásokkal van összekötve az összes többivel, ezért mindegy, hogy melyik 2–2 pontra kötjük a telepeket, és milyen polaritással – mindig ugyanazt a feladatot kell megoldanunk.
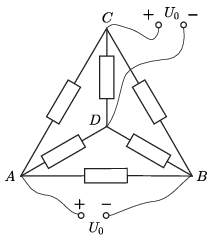
1. ábra \(\displaystyle \qquad\) \(\displaystyle \qquad\) \(\displaystyle \qquad\) \(\displaystyle \qquad\) \(\displaystyle \qquad\)2. ábra \(\displaystyle \qquad\) \(\displaystyle \qquad\) \(\displaystyle \qquad\) \(\displaystyle \qquad\) \(\displaystyle \qquad\)3. ábra \(\displaystyle \qquad\) \(\displaystyle \qquad\) \(\displaystyle \qquad\) \(\displaystyle \qquad\) \(\displaystyle \qquad\)4. ábra
A szuperpozíció-tételt fogjuk alkalmazni, ami szerint hálózatunkban, ha több generátor van, akkor ezek együttes hatása egy ellenálláson a következőképp határozható meg: A generátorok hatását egyenként vesszük figyelembe, miközben a többi feszültséggenerátort rövidzárral, az áramgenerátorokat pedig szakadással helyettesítjük, majd az így kapott eredményeket előjelhelyesen összegezzük. A telepeket, mivel belső ellenállásuk elhanyagolható, feszültséggenerátornak tekintjük.
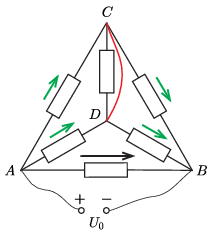
Először oldjuk meg tehát a tetraédert az \(\displaystyle A\) és \(\displaystyle B\) pontok közti első teleppel, miközben a \(\displaystyle C\) és \(\displaystyle D\) pontok közti második telepet rövidzárral helyettesítettük (2. ábra). Az \(\displaystyle AB\) ágban folyó áram Ohm törvénye szerint:
\(\displaystyle I=\frac{U_0}{R},\)
az \(\displaystyle AC\), \(\displaystyle BC\), \(\displaystyle AD\) és \(\displaystyle BD\) ágakban pedig
\(\displaystyle \frac{\frac{1}{2}U_0}{R}=\frac{1}{2}I.\)
A kétféle áramerősséget az ellenállások mellé rajzolt hosszabb (fekete), illetve rövidebb (zöld) nyilakkal jelöltük. A \(\displaystyle CD\) ellenálláson a rövidzár miatt nem folyik áram.
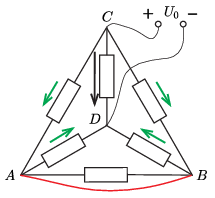
A második telep a hozzá képest azonos helyzetben levő ágakban pont ugyanekkora áramokat hoz létre (3. ábra).
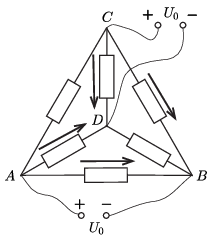
A 4. ábrán összeadtuk az előző kettőn berajzolt áramokat, figyelve az áramirányokra. Az \(\displaystyle AC\) és \(\displaystyle BD\) ágakban a két összetevő kiejti egymást, itt nem folyik áram. A többi négy ágban egyformán \(\displaystyle I=U_0/R\). Ezekben az ágakban a teljesítmény egyenként \(\displaystyle P=U_0I=U_0^2/R\). Végül tehát a \(\displaystyle T\) idő alatt az egész hálózaton fejlődő hő:
\(\displaystyle Q=\frac{4TU_0^2}{R}.\)
II. megoldás. A síkban kiterített kapcsolást az 5. ábra mutatja.
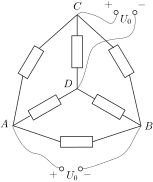
5. ábra
Mit állíthatunk az egyes csomópontok potenciáljáról? Bármelyik csomópontot ,,leföldelhetjük'', a potenciálját nullának választhatjuk. Legyen ez mondjuk a \(\displaystyle D\) csomópont. Ekkor a \(\displaystyle C\) pont potenciálja a rákapcsolt telep miatt \(\displaystyle U_0\) lesz. A másik két csomópontról azt tudjuk, hogy ha \(\displaystyle A\) potenciálja valamekkora, később meghatározandó \(\displaystyle U\), akkor a \(\displaystyle B\) ponté \(\displaystyle U-U_0\) (6. ábra). Az ábrán feltüntettük az egyes ellenállásokon folyó áramok erősségét is.
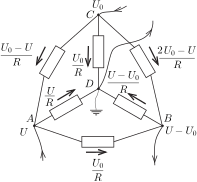
6. ábra
Az eddig ismeretlen \(\displaystyle U\) értékét a Kirchhoff csomóponti törvényéből határozhatjuk meg. Az \(\displaystyle A\) csomópontba például a telep pozitív pólusán keresztül ugyanannyi áram folyik be, amennyi a \(\displaystyle B\) pontnál a negatív pólus felé kifolyik:
\(\displaystyle \frac{U_0}{R}+\frac{U}{R}-\frac{U_0-U}{R}=\frac{U_0}{R}-\frac{U-U_0}{R}+\frac{2U_0-U}{R},\)
ahonnan kapjuk, hogy
\(\displaystyle 2U=4U_0-2U,\)
vagyis
\(\displaystyle U=U_0.\)
Ugyanezt az eredményt kapjuk, ha a \(\displaystyle C\) és a \(\displaystyle D\) csomópontokra alkalmazzuk a Kirchhoff törvényét.
A csomópontok potenciáljának (és így az egyes ágakra eső feszültségek) ismeretében leolvashatjuk, hogy a \(\displaystyle CA\) és a \(\displaystyle BD\) ágakban nem folyik áram, a többi négy ágban pedig \(\displaystyle I=U_0/R\) az áramerősség nagysága. Ezek szerint a teljes áramkör hőteljesítménye \(\displaystyle 4U_0I=4U_0^2/R\), és ennek megfelelően \(\displaystyle T\) idő alatt
\(\displaystyle Q=4 U_0^2T/R\)
Joule-hő fejlődik.
Megjegyzések. 1. A hőteljesítményt úgy is megkaphatjuk, hogy megállapítjuk: mindkét telepen \(\displaystyle 2I=2U_0/R\) áram folyik keresztül, a telepek által leadott összteljesítmény \(\displaystyle 2\cdot 2IU_0=4U_0^2/R.\)
2. Ha valamelyik telep polaritását felcseréljük, a fentiekkel megegyező eredményt kapjuk, vagyis azt, hogy két ellenálláson nem folyik áram, négyen pedig \(\displaystyle U_0/R\) az áram erőssége, de az ellenállások ,,szereposztása'' megváltozik.
Statisztika:
28 dolgozat érkezett. 4 pontot kapott: Bertollo Antonio, Blaskovics Ádám, Bogdán Balázs Ákos, Hornyák Zalán Zétény, Horváth Péter, Kovács Tamás , Lakatos Levente, Molnár Lili, Nyitrai Csenger, Sipeki Andor, Tajta Sára, Tasnádi Zsófia, Zádori Gellért. 3 pontot kapott: Békési Máté, Bense Tamás, Fuchs Vince, Kovács Dániel, Nagy Gellért Ákos, Papp Emese Petra, Wolf Erik. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 1 versenyző.
A KöMaL 2025. decemberi fizika feladatai

