A P. 5695. feladat (2025. december)

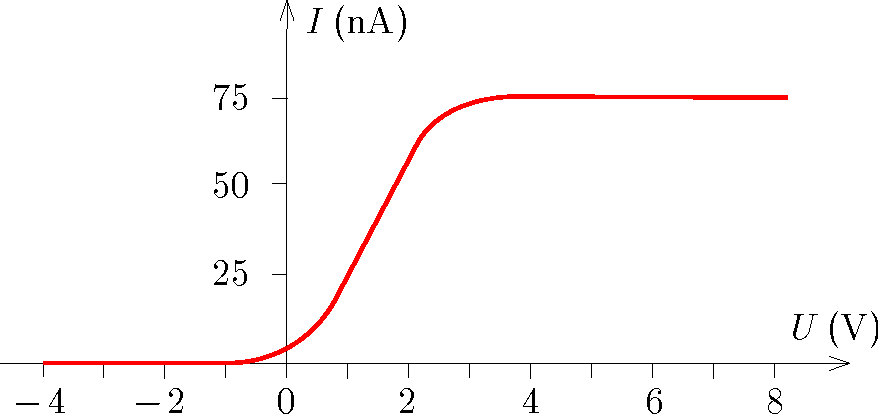
P. 5695. Állandó teljesítményű, 420 nm hullámhosszúságú fénynyalábbal cézium katódú vákuum-fotocellát világítunk meg. Az alábbi grafikon mutatja a fotocella fotoáramának \(\displaystyle I\) erősségét az anód katódhoz viszonyított \(\displaystyle U\) feszültségének függvényében.

a) Mekkora a cézium kilépési munkája?

b) Legalább mekkora teljesítményű fénynyaláb érkezett a fotocella katódjára?

Tornyai Sándor fizikaverseny, Hódmezővásárhely

(4 pont)

A beküldési határidő 2026. január 15-én LEJÁRT.

Megoldás. a) A fénynyaláb fotonjainak energiája \(\displaystyle h\nu=\tfrac{hc}{\lambda}\), ahol \(\displaystyle h=6{,}63\cdot 10^{-34}\,\mathrm{Js}\) a Planck-állandó, \(\displaystyle \nu\) a fény frekvenciája, \(\displaystyle c=3\cdot 10^8\,\mathrm{\tfrac{m}{s}}\) a fénysebesség és \(\displaystyle \lambda=420\,\mathrm{nm}=4{,}2\cdot 10^{-7}\,\mathrm{m}\) a fény hullámhossza. Ha egy foton elnyelődik a katódban, akkor annak energiája egyrészt fedezi a \(\displaystyle W_\mathrm{ki}\) kilépési munkát, másrészt mozgási energiát ad a kilökődő elektronnak. Ha elegendően nagy ellenfeszültséget kapcsolunk a fotocellára, akkor az megakadályozza, hogy az elektronok elérjék az anódot. Ez alapján

\(\displaystyle W_\mathrm{ki}=h\nu+Ue,\)

ahol \(\displaystyle U<0\) az a feszültség, ahol megszűnik az áram, \(\displaystyle e=1{,}60\cdot 10^{-19}\) pedig az elemi töltés. A grafikonról leolvasható, hogy \(\displaystyle U=-1\,\mathrm{V}\) (1 V nagyságú ellenfeszültség) esetén szűnik meg teljesen az áram. Ez alapján a cézium kilépési munkája:

\(\displaystyle W_\mathrm{ki}=h\nu+Ue=\frac{hc}{\lambda}+Ue\approx 3{,}1\cdot 10^{-19}\,\mathrm{J}.\)

Megjegyzés. A kilépési munkát gyakran elektronvoltban mérik. \(\displaystyle 1\,\mathrm{eV}\) az a munka, amelyet \(\displaystyle 1\,\mathrm{V}\) feszültség végez egy elemi töltésen, tehát \(\displaystyle 1\,\mathrm{eV}=1{,}60\cdot 10^{-19}\,\mathrm{J}\). A feladatunkban szereplő foton energiája elektronvoltban mérve: \(\displaystyle E_\gamma=\tfrac{hc}{e\lambda}=2{,}96\,\mathrm{eV}\), a cézium kilépési munkája pedig \(\displaystyle W_\mathrm{ki}=E_\gamma-U=1{,}96\,\mathrm{eV}\).

b) Kellően nagy gyorsítófeszültség esetén esetén az összes kilépő elektron eléri az anódot. A telítési áram megadja a másodpercenként kilépő elektronok számát, és ezzel együtt az elnyelődő (elektront kilökő) fotonok számát is: \(\displaystyle n=\tfrac{I}{e}\). A beérkező fénynyaláb minimális teljesítménye a fotonok számának és egy foton energiájának szorzata. A grafikonról leolvasható, hogy a telítési áram \(\displaystyle I=75\,\mathrm{nA}=7{,}5\cdot 10^{-8}\,\mathrm{A}\), amiből a fénynyaláb minimális teljesítménye:

\(\displaystyle P=nh\nu=\frac{Ihc}{e\lambda}=2{,}2\cdot 10^{-7}\,\mathrm{W}=0{,}22\,\mu\mathrm{W}.\)

(A fény egy része nem éri el a katódot, vagy visszaverődik róla, így a fénynyaláb teljesítményének ez a minimális értéke, ennél lehet nagyobb.)

Statisztika:

17 dolgozat érkezett.
4 pontot kapott:	Bertollo Antonio, Ferencz Kevin, Fuchs Vince, Horváth Péter, Kossár Benedek Balázs, Kovács Tamás , Kovács Tamás, Lakatos Levente, Tasnádi Zsófia, Vértesi Janka, Winhoffer Júlia, Zádori Gellért, Zólomy Csanád Zsolt.
3 pontot kapott:	Hornok Máté.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	1 versenyző.

A KöMaL 2025. decemberi fizika feladatai