 |
A P. 5696. feladat (2025. december) |
P. 5696. Vákuumban függőlegesen elhelyezkedő, hosszú, egyenes vezetőben időben állandó áram folyik. A vezetőtől \(\displaystyle r_0\) távolságra lévő \(\displaystyle P\) pontból az ábra szerint egy protont indítunk az egyenes vezetőre és a \(\displaystyle P\) pontra illeszkedő síkra merőleges irányban. Mozgása során a proton maximális távolsága a vezetőtől \(\displaystyle 4r_0\).
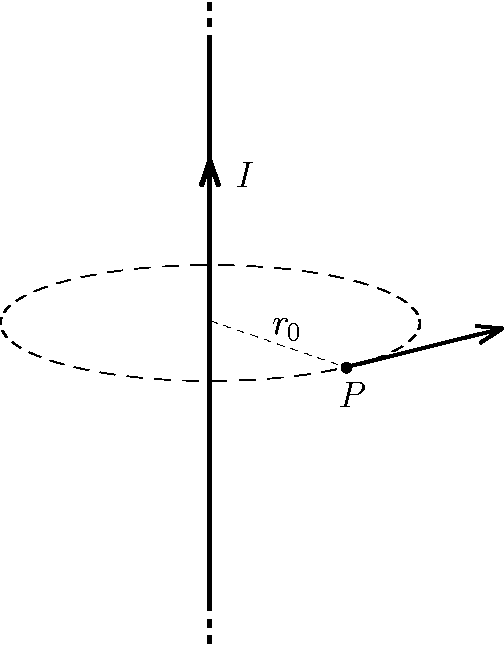
a) A mozgás során mekkora maximális \(\displaystyle \vartheta\) szöget zár be a proton mozgásiránya a vízszintessel?
b) Mekkora a \(\displaystyle \vartheta\) szög abban a pillanatban, amikor a proton \(\displaystyle 2r_0\) távolságra van az egyenes vezetőtől?
Közli: Vigh Máté, Herceghalom
(6 pont)
A beküldési határidő 2026. január 15-én LEJÁRT.
Megoldás. A proton mozgását egy olyan hengerkoordináta-rendszerben írjuk le, amelynek a \(\displaystyle z\) tengelye egybeesik a függőleges vezető tengelyével. Jelölje \(\displaystyle r\) a proton távolságát a tengelytől, és legyen \(\displaystyle z\) a függőleges elmozdulás! A proton sebességének a komponensei ebben a rendszerben \(\displaystyle (v_r,\,v_\varphi,\,v_z)\). A vezetőben folyó áram hatására létrejövő mágneses indukció \(\displaystyle \varphi\) irányú, azaz minden pontban az adott pont és a \(\displaystyle z\) tengely által meghatározott \(\displaystyle (r,z)\) síkra merőleges, és az \(\displaystyle r\) távolság reciprokával arányos, tehát
\(\displaystyle B=\frac{r_0}{r}B_0\)
alakú. (Itt \(\displaystyle B_0\) kifejezhető az áram segítségével, de nem érdemes ezze bajlódni, hisz azt sem ismerjük.) A Lorentz-erő merőleges a pillanatnyi sebességre, ezért nem változtatja meg annak a nagyságát, tehát
\(\displaystyle \sqrt{v_r^2+v_\varphi^2+v_z^2}=v_0.\)
Másrészről a Lorentz-erő merőleges a mágneses indukcióra is, ezért a proton és a \(\displaystyle z\) tengely közös síkjában hat, így nincs forgatónyomatéka a tengelyre vonatkozóan. Ebből következik, hogy a protonnak a \(\displaystyle z\) tengelyre vonatkozó impulzusmomentuma állandó, tehát a kezdeti feltételeket is figyelembe véve
\(\displaystyle rv_\varphi=r_0v_0,\qquad\textrm{azaz}\qquad v_\varphi=v_0\frac{r_0}{r}.\)
a) A sebesség vízszintessel bezárt \(\displaystyle \vartheta\) szöge a sebesség függőleges komponensével van összefüggésben:
\(\displaystyle \sin\vartheta=\frac{v_z}{v_0}.\)
\(\displaystyle v_z\)-t a többi sebességkomponenssel kifejezve, és \(\displaystyle v_\varphi\)-t behelyettesítve
\(\displaystyle v_z=v_0\sqrt{1-\left(\frac{v_r}{v_0}\right)^2-\left(\frac{r_0}{r}\right)^2}.\)
Amikor \(\displaystyle r\) maximális, akkor \(\displaystyle v_r\) éppen eltűnik, tehát a sebesség függőleges komponensének a maximális értéke
\(\displaystyle v_{z,\mathrm{max}}=v_0\sqrt{1-\left(\frac{r_0}{r_\mathrm{max}}\right)^2}.\)
Ebből a legnagyobb \(\displaystyle \vartheta\)
\(\displaystyle \vartheta_\mathrm{max}=\arcsin{\sqrt{1-\left(\frac{r_0}{r_\mathrm{max}}\right)^2}}=\arcsin{\sqrt{\frac{15}{16}}}=75{,}5^\circ.\)
b) A \(\displaystyle \vartheta\) közbülső értékeinek a meghatározásához a \(\displaystyle v_z\) egyenletéből kell kiindulnunk. A Lorentz-erő, ami az \(\displaystyle (r,z)\) síkban hat, nagysága arányos az \(\displaystyle e\) töltéssel, a \(\displaystyle B\)-vel és a sebesség \(\displaystyle (r,z)\) síkra vett \(\displaystyle (v_r,0,v_z)\) vetületével, de merőleges arra, komponensekkel az
\(\displaystyle (F_r,F_\varphi,F_z)=\left(-ev_z\frac{r_0}{r}B_0,0,ev_r\frac{r_0}{r}B_0\right)\)
alakban adható meg. Ennek alapján a proton függőleges gyorsulása
\(\displaystyle a_z=\frac{er_0B_0}{m}\frac{v_r}{r}.\)
Az egyenlet bal oldalán az \(\displaystyle a_z\) definíció szerint a \(\displaystyle v_z\) változási sebessége (idő szerinti deriváltja), a jobb oldalon pedig \(\displaystyle v_r/r\) az \(\displaystyle \ln r\)-nek, azaz a tengelytől való távolság logaritmusának a deriváltja. Mindkét oldalt integrálva tehát a
\(\displaystyle v_z=\frac{er_0B_0}{m}\,\ln\frac{r}{r_0}\)
összefüggést kapjuk. Itt \(\displaystyle v_z\) és \(\displaystyle r\) a két mennyiségnek ugyanabban az időpillanatban felvett értékei (de az időfüggést nem jelöltük, mert nem ismerjük, és nincs is rá szükségünk), és kihasználtuk, hogy kezdetben, amikor \(\displaystyle r=r_0\), akkor \(\displaystyle v_z=0\). Ennek alapján
\(\displaystyle v_{z,\mathrm{max}}=\frac{er_0B_0}{m}\,\ln\frac{r_\mathrm{max}}{r_0}.\)
Az ismeretlen \(\displaystyle B_0\)-t kiküszöbölve és \(\displaystyle v_{z,\mathrm{max}}\) értékét behelyettesítve a
\(\displaystyle v_z=\frac{v_0\sqrt{1-\left(\frac{r_0}{r_\mathrm{max}}\right)^2}\,\ln\frac{r}{r_0}}{\ln\frac{r_\mathrm{max}}{r_0}}\)
kifejezést kapjuk, aminek a segítségével
\(\displaystyle \sin\vartheta(r)=\frac{\sin\vartheta_\mathrm{max}\,\ln\frac{r}{r_0}}{\ln\frac{r_\mathrm{max}}{r_0}}.\)
Eszerint akkor, amikor \(\displaystyle r=2r_0\),
\(\displaystyle \sin\vartheta(2r_0)=\frac{\sin\vartheta_\mathrm{max}}{2},\qquad\textrm{azaz}\qquad\vartheta(2r_0)=29{,}0^\circ.\)
Statisztika:
13 dolgozat érkezett. 6 pontot kapott: Beke Márton Csaba, Erdélyi Dominik, Simon János Dániel, Tasnádi Zsófia, Winhoffer Júlia, Zádori Gellért, Zólomy Csanád Zsolt. 4 pontot kapott: 2 versenyző. 2 pontot kapott: 2 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2025. decemberi fizika feladatai

