 |
Az S. 109. feladat (2016. szeptember) |
S. 109. Egy vállalat \(\displaystyle N\) embert foglalkoztat. Mindenkinek legfeljebb két beosztottja (akiknek a sorrendje nem fontos), és pontosan egy felettese van, kivéve a főigazgatót, akinek nincs felettese. A munkatársakat az \(\displaystyle 1,\ldots, N\) számokkal azonosítjuk, az 1-es a főigazgató. A cég súlyos pénzügyi gondokkal küzd, ezért elhatározták, hogy átszervezik a beosztás rendszerét. Ehhez felvehetnek új munkatársakat, illetve megválhatnak bizonyos alkalmazottaktól. Ezenkívül az egyedüli megengedett művelet az azonosítószámok átírása. Minden egyes új munkatárs felvételéhez állásinterjút kell szervezni \(\displaystyle F\) krajcárért, valamint tudjuk, hogy az \(\displaystyle i\)-edik alkalmazott elbocsátása a végkielégítés miatt \(\displaystyle V[i]\) krajcárba kerül. Az azonosítók átírásának természetesen nincs költsége.
A cégvezetés megadta, hogy szerintük mi az optimális vállalati struktúra. A fenti feltételek erre a szerkezetre is igazak. Írjunk programot, ami megadja, hogy legalább hány krajcárt kell elkölteni az átalakításra.
A standard bemenet első sora az alkalmazottak \(\displaystyle N\) számát és egy új alkalmazott felvételének \(\displaystyle F\) költségét tartalmazza. A második sor \(\displaystyle N\) egész számot tartalmaz, az \(\displaystyle i\)-edik szám \(\displaystyle V[i]\), vagyis az \(\displaystyle i\)-edik alkalmazott végkielégítése. A harmadik sor \(\displaystyle N-1\) számot tartalmaz, az \(\displaystyle i\)-edik szám az \(\displaystyle (i+1)\)-edik beosztott felettesének a száma. A negyedik és ötödik sor az átalakítás után elérni kívánt struktúrát írja le: a negyedikben az alkalmazottak kívánt \(\displaystyle M\) száma található, míg az ötödikben \(\displaystyle M-1\) egész szám írja le a feletteseket a harmadik sorhoz hasonló módon.
A standard kimenet első és egyetlen sora tartalmazza az átalakítás minimális \(\displaystyle K\) költségét.
Korlátok: \(\displaystyle 1\le N\), \(\displaystyle M\le 5000\); \(\displaystyle 0\le V[i]\), \(\displaystyle F\le 10^5\); időlimit: 0,2 mp; memórialimit: 256 MB.
A verem (stack) méretére nincs külön korlát, ez is a teljes memóriába számít bele.
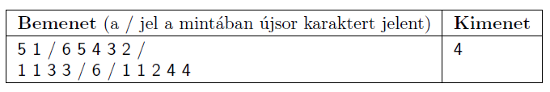
Magyarázat: elbocsátjuk a 5-ös számú alkalmazottat, és a 4-es számú alá felveszünk két új beosztottat. Ekkor a költség \(\displaystyle V[5]+2\cdot F = 2+2\cdot 1 = 4\). Ha átnevezzük a 2-est 3-assá, a 3-ast 2-essé, akkor megkapjuk a kívánt struktúrát.
Pontozás és korlátok: a programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani a fenti korlátoknak megfelelően.
Beküldendő egy tömörített s109.zip állományban a program forráskódja, valamint a program rövid dokumentációja, amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.
(10 pont)
A beküldési határidő 2016. október 10-én LEJÁRT.
Használjuk a dinamikus programozás módszerét. Az első fa minden \(\displaystyle i\) pontjára és a második fa minden \(\displaystyle j\) pontjára tároljuk az \(\displaystyle i\)-edik pont által meghatározott részfának a \(\displaystyle j\)-edik pont által meghatározott részfává alakítás minimális költségét (dp[i][j]).
Ha az üres részfát felvesszük egy speciális pontként, akkor összesen három eset van:
1) Üres részfát üres részfává ingyen átalakíthatjuk
Ha valamelyik részfa nem üres, akkor
2) a bal részfát a bal részfává, a jobb részfát a jobb részfává alakíthatjuk, vagy
3) a jobb részfát a bal részfává a bal részfát a jobb részfává alakíthatjuk
A második és a harmadik eset függ a fában a két pont gyerekeire kiszámított értékektől. (A pontos képletek a mintamegoldásban olvashatók)
A kiszámítás sorrendjére használhatjuk a mélységi bejárás szerinti elhagyási sorrendet (mivel így a gyerekekre előbb számítódik ki az érték, mint a szülőre), vagy még egyszerűbb, ha dinamikus programozás helyett rekurzívan oldjuk meg a feladatot memorizálással. A mintamegoldás az utóbbi módon működik.
A futási idő \(\displaystyle O(n\cdot m)\), a megoldás \(\displaystyle O(n\cdot m)\) memóriát használ.
Statisztika:
17 dolgozat érkezett. 10 pontot kapott: Alexy Marcell, Bálint Martin, Busa 423 Máté, Csenger Géza, Gáspár Attila, Gergely Patrik, Horváth 546 János, Janzer Orsolya Lili, Kovács 246 Benedek, Nagy Ábel, Németh 123 Balázs, Noszály Áron, Olexó Gergely, Szakali Benedek. 6 pontot kapott: 1 versenyző. 3 pontot kapott: 1 versenyző. 1 pontot kapott: 1 versenyző.
A KöMaL 2016. szeptemberi informatika feladatai

