Az S. 44. feladat (2009. április)

S. 44. Bergengóciában minden évben megrendezésre kerül a Nemzeti Villamoshajtó Bajnokság, a királyság legnevesebb versenysorozata. Ennek keretében minden nagyváros egy-egy versenyt rendez, melynek helyszíne a város leghosszabb villamospályája. A versenyzők egyesével indulnak, céljuk, hogy a lehető legrövidebb idő alatt végighaladjanak a pályán.

Bár a verseny ideje alatt az utasszállítás szünetel, a teljes közúti forgalmat még egy ekkora attrakció kedvéért sem lehet leállítani. A szörnyű balesetek elkerülése érdekében ezért a versenyzők a kereszteződéseknél a piros jelzésen a verseny során sem haladhatnak át.

Írjunk programot, mely meghatározza, hogy optimális esetben mennyi idő alatt teljesíthető a teljes táv. A program a pálya leírását fájlból olvassa, az eredményt fájlba írja. A bemeneti, illetve kimeneti fájlok nevei az első, illetve második parancssori argumentumok.

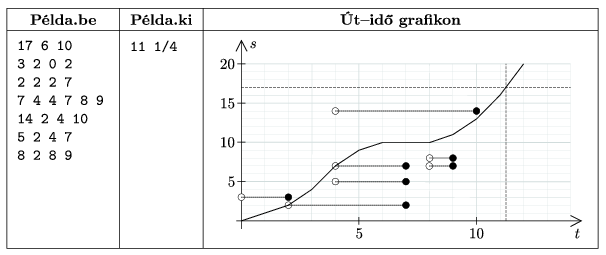
A villamos eleje az x=0 koordinátájú pontból indul a t=0 időpillanatban, és minden időegység kezdetén -1, 0, +1 egységgel változtathatja (pillanatszerűen) a sebességét, mellyel ezután egységnyi ideig egyenletesen halad az x tengely mentén. A villamos megállhat, de nem tolathat és nem is lépheti túl az M maximális sebességet.

A kereszteződéseknél a villamos elejének kell a zöld jelzésen áthaladni, a lámpa állapotaihoz balról nyílt, jobbról zárt időintervallumok tartoznak. (Tehát az éppen pirosra váltó lámpán a villamos még áthaladhat, de az éppen zöldre váltón még nem.) Célba érkezésnek azt a pillanatot tekintjük, amikor a villamos elejének x koordinátája megegyezik a pálya L hosszával.

A bemenet első sorában három, szóközzel elválasztott szám szerepel: a pálya 10 $\le$ L $\le$ 5000 hossza, a lámpák 0 $\le$ N $\le$ 1000 száma, illetve a villamos 1 $\le$ M $\le$ 30 végsebessége. Az ezt követő N db sor mindegyikében egy-egy lámpa leírása következik: a lámpa 1 $\le$ X_i $\le$ L pozíciója, állapotváltásainak 1 $\le$ C_i $\le$ 100 száma (de összesen legfeljebb 1000 állapotváltás), majd C_i db szám, az egyes piros-zöld állapotváltások $0\le T_{i,j} \le 10\;000$ időpontja, mind szóközzel elválasztva. Kezdetben minden lámpa zöld jelzést mutat.

A kimenetben egyetlen szám szerepeljen: a teljes táv megtételéhez minimálisan szükséges idő egészrész-törtrész alakban ( $a \ b/c$ ), ahol c a célba érkezés sebessége.

A maximális pontszám eléréséhez a programnak a legnagyobb tesztesetekre is néhány percen belül le kell futnia (egy korszerű PC-n). A feladat 64kB memóriában is megoldható, ezért az időkorlát az ilyen környezetekben készült megoldásokra is vonatkozik, így (átmeneti) segédfájlok használatát ott sem javasoljuk.

Beküldendő a program forráskódja (s44.pas, s44.cpp, ...), valamint a program rövid dokumentációja (s44.txt, s44.pdf, ...). A dokumentáció tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztőkörnyezetben fordítható és hogyan paraméterezhető.

Figyelem: A feladat szövege az "áthaladás" szót használja a villamos és a kereszteződések (lámpák) viszonyának leírásához, mely álló villamos esetén nehezen értelmezhető. Ezekben az esetekben tekintsük úgy, hogy a villamos az egy helyben állás teljes időtartama alatt, a végpontokat is beleértve, minden pillanatban "áthalad" a kereszteződésen.

(10 pont)

A beküldési határidő 2009. május 15-én LEJÁRT.

A megoldás menete

A feladat megoldásához célszerű volt bevetni a dinamikus programozás módszerét. A módszert olyan optimalizációs feladatok esetén célszerű alkalmazni, ahol a teljes probléma optimális megoldása felírható valamilyen részproblémák megoldásainak ismeretében, illetve egy-egy részmegoldásra többször is szükség van.

Formalizáljuk tehát a feladatot a következőképp. Legyen P[t,x,v] az ún. elérhetőségi mátrix: egy olyan háromdimenziós, logikai értékekből álló táblázat, melynek (t,x,v) eleme akkor és csak akkor igaz, ha a villamos a t időpillantban érkezhet v sebességgel az x koordinátájú pontba. A feladat ennek a mátrixnak a kitöltése. Ha ez megvan (elegendő t időig), akkor mindössze annyit kell tennünk az eredeti feladat megoldásához, hogy megvizsgáljuk, hogy melyik legkisebb t₁ értéknél van először x $\ge$ L pozícióhoz tartozó cellában igaz érték. Ha több ilyen is van, akkor azt kiválasztjuk, amelyhez tartozó út a legkorábban metszi az x=L egyenest.

De hogyan töltsük ki a táblázatot? A t=0-hoz tartozó cellák kitöltése egyszerű: P[0,0,0]=igaz, minden más x és v-re P[0,x,v]=hamis, hiszen tudjuk, hogy t=0-ban a villamos az origóban áll. Definiáljunk továbbá egy L[t,x] függvényt, mely igaz, ha a t időben az x helyen a lámpa piros. A további értékek kitöltése így magától értetődik:

$P[t,x,v] = \left(P[t-1,x-v,v-1]~vagy~P[t-1,x-v,v]~vagy~P[t-1,x-v,v+1]\right)~es~\left(!L[t,x'], x' \in \{x\}\cup\{x-v+1,...,x-1\}\right)$

feltéve, hogy az értelmezési tartományon kívül koordinátákra P[t,x,v]=0. Érdemes megfigyelni, hogy a t+1. időszelet kitöltéséhez elegendő csupán a t. időszelet értékeit ismerni: tehát nem szükséges az egész mátrixot eltárolni, elegendő csupán 2 szeletét... vagy akár 1 szeletét, ha megoldjuk, hogy ne írják felül egymást az értékek (pl. jó sorrendben frissítjük).

A megoldások értékelése

A megoldások nagy része backtracking módszerrel kísérelte meg a feladatot megoldani, azonban ezek a megoldások a megfelelő korlátozó feltételek híján már a közepes méretű bemenetekre sem futottak le időben. Volt azonban néhány dinamikus programozást használó megoldás is, melyeknek nagyon örültünk.

Rendkívül sok megoldás esetén találkoztunk implementációs hibákkal -- gyakran olyan súlyosakkal, melyek hatására majd' az összes tesztbemenetre hibás eredmény született. A hibák általában elírásból, elnézésből fakadnak, ezért nem győzzük hangsúlyozni annak fontosságát, hogy a programokat beadás előtt magatok is teszteljétek!

Mintamegoldás, tesztesetek, szemléltetőprogram

Pascal mintamegoldás, Englert Péter, 12. osztályos versenyző (Zrínyi Miklós Gimnázium, Zalaegerszeg) munkája alapján: englert.zip

Hivatalos mintamegoldás C++ nyekven: mmo.cpp

Tesztesetek: javit.zip

Interaktív szemléltetőprogram: TestGenerator.zip

Statisztika:

13 dolgozat érkezett.

10 pontot kapott: Véges Márton.

8 pontot kapott: 2 versenyző.

7 pontot kapott: 2 versenyző.

6 pontot kapott: 2 versenyző.

5 pontot kapott: 4 versenyző.

4 pontot kapott: 2 versenyző.

A KöMaL 2009. áprilisi informatika feladatai

13 dolgozat érkezett.
10 pontot kapott:	Véges Márton.
8 pontot kapott:	2 versenyző.
7 pontot kapott:	2 versenyző.
6 pontot kapott:	2 versenyző.
5 pontot kapott:	4 versenyző.
4 pontot kapott:	2 versenyző.

Már regisztráltál?
Új vendég vagy?