Az S. 56. feladat (2010. október)

S. 56. Adott egy város úthálózata a csomópontokkal (kereszteződésekkel), illetve az ezeket összekötő kétirányú utcákkal. Egy olyan városnéző busszal szeretnénk bejárni a város összes csomópontját (az utcák közül nem kell mindet bejárni), amelynek elromlott a hátramenete, így nem tud megfordulni, azaz nem térhet vissza abba a csomópontba, amelyikből éppen most jött (egyébként bármely utcán, illetve csomóponton bárhányszor járhatunk).

Írjunk programot, amely beolvassa a standard bemenetről a város úthálózatának leírását, és meghatározza a csomópontoknak egy olyan sorozatát, amelyben szerepel minden csomópont, az egymás utáni csomópontok közvetlen összeköttetésben állnak, és nincs benne ,,megfordulás'', azaz olyan három egymás utáni csomópont, amelyekből az első és a harmadik megegyezik. Feltehetjük, hogy bármely két csomópont közt legfeljebb egy utca vezet, hogy a város úthálózata összefüggő (azaz a város bármely pontjából bármely pontjába eljuthatunk), továbbá hogy nincs a városban zsákutca, azaz nincs olyan csomópont, amihez csak egy utca kapcsolódik.

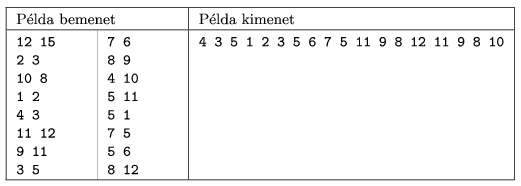
A bemenet szerkezete a következő: az első sorban két, szóközzel elválasztott egész szám, a város csomópontjainak () és az utcáinak () száma található. A következő M sor mindegyikében, szóközzel elválasztva, egy-egy utca két végpontjának X_i, Y_i sorszáma szerepel (1X_iY_iN).

A standard kimenet egyetlen sorába írjuk ki a feladat feltételeinek megfelelő csomópontsorozatot.

Beküldendő a feladat megoldását tartalmazó forrás és projektállományok (az .exe és más a fordító által generált kiegészítő állományok nélkül), valamint a megoldás menetét röviden bemutató dokumentáció (s56.txt, s56.pdf, ...) egy tömörített mappában (s56.zip).

(10 pont)

A beküldési határidő 2010. november 10-én LEJÁRT.

A feladatot háromféleképpen is meg lehetett oldani.

1. A legegyszerűbb megoldás a következő: Elindulunk az első csúcsból, folyamatosan számon tartjuk, hogy melyik csúcsban hányszor jártunk, és az aktuális csúcsnak mindig abba a szomszédjába lépünk, amelyikben eddig a legkevesebbszer voltunk (a szomszédok közül nem vesszük figyelembe a megfordulási feltétel által kizárt csúcsot). Az algoritmus akkor ér véget, ha már bejártunk minden csúcsot (ennek ellenőrzéséhez számon tartjuk, hogy hány csúcsban jártunk már). Erről nem könnyű belátni, hogy mindig eredményt ad, azaz hogy nem kerülhet esetleg végtelen ciklusba. A bizonyítás és a forráskód: egyszeru.zip. A beküldött megoldások között nem volt 100 sor alatti, viszont ez a megoldás kevesebb, mint 50 sorban megírható.

2. A mélységi bejárást használó megoldást Borsos Zalán 12. osztályos marosvásárhelyi versenyzőnek sikerült tökéletesre megcsinálnia. DFS.zip

3. A széltében kereséses megoldás senkinek sem sikerült tökéletesre. Többféle elvi, illetve implementálási hiba előjött. Adrián Patrik 11. osztályos debreceni tanulónak csak az implementációban volt hiba, úgyhogy az ő megoldásának javított változatát adjuk közre. BFS.zip Volt olyan, aki az egész széltében keresésből kizárta a legutóbb meglátogatott csúcsot (ahelyett, hogy csak a kiinduló csúcs szomszédai közül zárta volna ki). Ez hibát okoz pl. ebben a tesztesetben, be1.txt amikor az 1, 2, 3 csúcsok bejárása után a 4-es csúcsba kéne eljutni. Olyan is volt, aki mindig előre kijelölte, hogy melyik csúcsba szeretne menni. Ez azért okoz hibát, mert nem biztosított, hogy minden széltében keresésnél el tudunk jutni az összes csúcsba.

Maximális méretű bemenetekre a futási idők az alábbiak körül alakultak (tized mp-ben):

Ritka gráfokra (kb. 60000 él): 1. megoldás: 5, 2. megoldás: 50, 3. megoldás: 4

Sűrűbb gráfokra (kb. 500000 él): 1. megoldás: 25, 2. megoldás: 16, 3. megoldás: 50

A leghosszabb sétákat általában a mélységi bejárásos megoldás adta (10000 csúcsú, ritka gráfokra több százszor hosszabbakat, mint a másik két megoldás). Az 1. megoldás által adott út hossza minden tesztesetnél belül volt a gráf csúcsszámának 2.125-szörösén.

Voltak, akik backtrack-el próbálkoztak de ezek a megoldások túl lassúak voltak nagyobb tesztesetekre.

Statisztika:

9 dolgozat érkezett.
10 pontot kapott:	Borsos 607 Zalán.
9 pontot kapott:	Nagy 111 Miklós, Szabó 928 Attila.
7 pontot kapott:	3 versenyző.
6 pontot kapott:	1 versenyző.
4 pontot kapott:	1 versenyző.
3 pontot kapott:	1 versenyző.

A KöMaL 2010. októberi informatika feladatai