A KöMaL 2020. februári informatika feladatai

I-jelű feladatok A beküldési határidő 2020. március 10-én LEJÁRT.

---

I. 502. A számegyenesen \(\displaystyle N\) darab intervallumot adunk meg. Az intervallumok nyíltak vagy zártak lehetnek, határpontjaik egészek vagy tizedes törtek. Jelölésük a szokásos módon történik (az informatikában megszokottabb tizedes pontot használva), például \(\displaystyle \left[4, 5.2\right[\) vagy \(\displaystyle \left]-3.3, 4.66\right[\), ahol az első intervallum balról zárt és jobbról nyílt, míg a második mindkét oldalról nyílt. Keressük meg a számegyenes azon egész számait, amelyek a legtöbb intervallumban vannak benne.

A program olvassa be a bemenet első sorából az intervallumok \(\displaystyle N\) számát (\(\displaystyle 2\le N\le 100\)), és a következő \(\displaystyle N\) sorból egyenként az intervallumokat. A bemenet intervallumai az egyszerűbb beolvasás céljából szóközökkel tagoltak a mintának megfelelően, valamint mind a \(\displaystyle [-1000, 1000]\) intervallum részei.

A kimenet egyetlen sorába írjuk ki növekvő sorrendben a legtöbb intervallumban szereplő egészeket. Az eredmény számait szóközökkel határoljuk, az egymást követő egészek sorozatának csak szélső értékeit adjuk meg kötőjellel elválasztva.

Példa Bemenet (a / jel sortörést helyettesíti)	Példa Kimenet
3 / [ -5.5 , 9 ] / ] 7 , 11.1 [ / ] 3 , 5 [	4 8 - 9

Beküldendő egy tömörített i502.zip állományban a megoldást tartalmazó forrásállomány, valamint egy rövid szöveges leírás, ami tájékoztat az alkalmazott programozási nyelvről és a fejlesztői környezetről.

Letölthető állomány: i502beki.zip (példa be- és kimenetek).

(10 pont)

megoldás, statisztika

---

I. 503. (É). Magyarország közigazgatási helynévkönyve egy 1992 óta évente megjelenő kiadvány, mely tartalmazza minden település hivatalos megnevezését, megyei beosztását, a közös önkormányzati hivatalokat, a helységek járási besorolását, valamint a nemzetiségi önkormányzatokat. Közli a helységek 2018. január 1-jei területnagyság-, lakónépesség- és lakásszámadatát, továbbá a helységek KSH által kibocsátott településazonosító törzsszámát. Feladatunk ezen adatok feldolgozása lesz táblázatkezelő program segítségével.

1. Töltsük be a települési adatokat tartalmazó hnk1_2018.txt szövegfájlt a táblázatkezelő egy munkalapjára az A1-es cellától kezdődően, a kódok jelentését tartalmazó hnk2_2018.txt szövegfájlt pedig egy másik munkalapra. A munkalapok neve legyen rendre adat és statisztika. Mindkét állomány pontosvesszővel tagolt, UTF-8 kódolású.

2. Munkánkat kozighelynev néven mentsük el a táblázatkezelő alapértelmezett formátumában.

3. A C3183-as cellától kezdődően egymás alá gyűjtsük ki a jogállásokat. Minden típust egyszer. A mellette lévő \(\displaystyle D\) oszlopban pedig másolható függvény segítségével adjuk meg, hogy az egyes jogállástípusokból hány található az országban.

4. Hozzunk létre egy új oszlopot a jelenlegi H oszlop mögé és ebben az oszlopban jelenjen meg az önkormányzati hivatali kód jelentése, ami a statisztika munkalapon található.

5. A statisztika munkalap C11:E11-es celláiban függvény segítségével adjuk meg Magyarország területét (hektárban), lakónépességét és a lakások számát. Ügyeljünk rá, hogy Budapest szerepel kerületenként lebontva is a listában.

6. Tudjuk, hogy legtöbben Budapesten laknak. A statisztika munkalap B9-es cellájában egész mondatba foglalva, függvények segítségével a lakosságszámot is megadva, írjuk ki annak a településnek a nevét, ami a második legnagyobb lakosságszámú.

7. Az előző mintájára a B10-es cellában adjuk meg annak a településnek a nevét, megyéjét, és lakosságszámát, ahol a legkevesebben laknak.

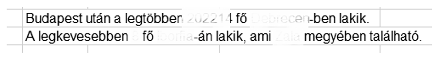
8. Az N oszlopban adjuk meg, hogy két tizedesjegyre felfelé kerekítve átlagosan hányan élnek egy lakásban.

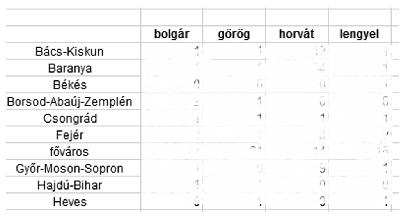
9. Készítsünk egy 21 soros, 14 oszlopos táblázatot a statisztika munkalapra az eredeti táblázat mellé, úgy, hogy a G3-as cellába ,,Bács-Kiskun'' megye kerüljön. Alatta gyűjtsük ki az adatok munkalap \(\displaystyle D\) oszlopában található ,,megye'' neveket és rendezzük ABC-rendbe. A H2-es cellába a ,,bolgár'' szó kerüljön, a mellette lévő cellákba a többi nemzetiségi önkormányzat az adat munkalapról. A táblázatot töltsük fel egyetlen másolható függvény használatával úgy, hogy megyénként adja meg az önkormányzatok számát.

10. A statisztika munkalapon található C oszlopban adjuk meg, hogy az egyes önkormányzati hivatalokhoz hány lakás tartozik.

Forrás: http://www.ksh.hu/apps/shop.kiadvany?p_kiadvany_id=1039140&p_lang=HU (2019.09.11.).

Beküldendő egy tömörített i503.zip állományban a megoldást adó táblázatkezelő munkafüzet és egy rövid dokumentáció, amely megadja a felhasznált táblázatkezelő nevét és verzióját.

Letölthető állományok: hnk12018.txt, hnk22018.txt.

(10 pont)

statisztika

---

I. 504. A középkorban használt titkosítási eljárások egyike a Cardano-rács. A titkosítandó szöveget ebben az esetben négyzet alakban rendezik el, a szöveg rejtjelezése és visszafejtése pedig az erre illeszkedő, megfelelő helyeken kivágott rostély ablakain keresztül történik. A szövegből a rácsban csak a betűk szerepelnek, az írásjelek és szóközök nem. A rostély egy-egy helyzetében a látható betűket sorfolytonosan kiolvassuk, a rostély háromszori körbefordításával a négyzet minden betűje felhasználásra kerül. (A dupla betűket két karakterrel kódoljuk, például GY helyett G és Y.)

A módszer bemutatása az I. 201. feladatban szerepelt, érdemes belenézni a kitűnő mintamegoldásokba (https://www.komal.hu/feladat?a=feladat&f=
I201&l=hu).

Készítsünk programot, amely a Cardano-ráccsal történő rejtjelezést és visszafejtést végzi el:

1. Olvassuk be és tároljuk el a Cardano-rácsot tartalmazó cardano.txt állományt, amely egy \(\displaystyle 6\times 6\)-os rostélyt tartalmaz. Az átlátszó rácspontokban 0 szerepel, a nem átlátszókban 1.

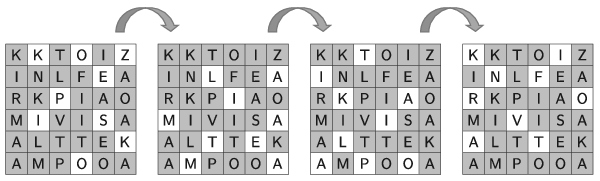
2. Készítsünk eljárást Forgat néven, amely lehetővé teszi a Cardano-rács \(\displaystyle -90\) fokos (vagyis az óramutató járásával egyező irányú) elforgatását.

3. Írassuk ki a képernyőre a megadott Cardano-rácsot, valamint annak \(\displaystyle -90\) fokos elforgatását. A két rács egymás alatt jelenjen meg.

4. A fenti mintán látható szöveget a titkos.txt fájl tartalmazza \(\displaystyle 6\times 6\)-os rácsokra bontva. Olvassuk be a fájl tartalmát, fejtsük vissza azt a megadott Cardano-rács segítségével a Forgat eljárás felhasználásával, majd a megfejtést sorfolytonosan írassuk ki a képernyőre.

Ha a titkosítandó szöveg ,,egy négyzetnél'' hosszabb, akkor azt több négyzetre kell bontani. Ha nem tesz ki a szöveg utolsó része egy teljes négyzetet, akkor azt véletlenszerű karakterekkel töltik fel.

A Cardano-rács alkalmazásával találkozhatunk Jules Verne: Sándor Mátyás c. könyvében is. A könyvben szereplő titkosítandó szöveget a nyilt.txt UTF-8 kódolású állomány tartalmazza. A könyvben a titkosítást két lépésben végezték, az alábbiakban ezt kell végrehajtani:

5. Olvassuk be a nyilt.txt fájl tartalmát, majd fordítsuk meg a szöveget. A beolvasott, illetve a megfordított szöveget egyaránt írassuk ki a képernyőre.

6. A felcserélt karakterekből álló szöveget rejtjelezzük a megadott Cardano-rács alkalmazásával, és az eredményt \(\displaystyle 6\times 6\)-os rácsban – a minta szerint – írassuk ki a sandormatyas.txt fájlba.

Beküldendő egy i504.zip tömörített állományban a program forráskódja és egy rövid leírás, ami megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

Letölthető fájlok: cardano.txt, nyilt.txt, titkos.txt.

(10 pont)

megoldás, statisztika

I/S-jelű feladatok A beküldési határidő 2020. március 10-én LEJÁRT.

---

I/S. 42. Egy út mindkét oldalán kilométerenként található egy-egy kilométerkő. \(\displaystyle N\) csirke szeretne átkelni az út egyik (ugyanazon) oldaláról a másikra. Mindegyikről tudjuk, hogy melyik kilométerkőtől indul és melyik kilométerkőhöz érkezik. Minden kilométerkőtől legfeljebb egy csirke indul és minden kilométerkőhöz legfeljebb egy csirke érkezik. Ha két csirke útvonala keresztezi egymást, akkor találkozhatnak, összezavarodnak és esetleg nem érnek célba. Adjuk meg, hány csirke útja biztonságos, tehát hányat nem fenyeget a keresztezésből adódó veszély.

Bemenet: az első sor tartalmazza a csirkék \(\displaystyle N\) számát. A következő \(\displaystyle N\) sor mindegyike két számot tartalmaz, mely azt jelenti, hogy az \(\displaystyle i\)-edik csirke az \(\displaystyle A_{i}\) kilométerkőtől indul és a \(\displaystyle B_{i}\) kilométerkőhöz érkezik.

Kimenet: az első sor tartalmazza azon csirkék számát, amelyek biztonságosan át tudnak kelni az úton.

Példa:

Korlátok: \(\displaystyle 1\le N\le {10}^{5}\), \(\displaystyle 1\le A_{i}, B_{i}\le {10}^{9}\). Időkorlát: 0,3 mp.

Értékelés: a pontok 50%-a kapható, ha \(\displaystyle N\le 10\,000\).

Beküldendő egy is42.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.

(10 pont)

statisztika

S-jelű feladatok A beküldési határidő 2020. március 10-én LEJÁRT.

---

S. 141. Egy épület legfelső emelete \(\displaystyle N\) darab lépcsőfokra van a földszinttől. Balázs \(\displaystyle M\) napon át, minden nap felmegy a földszintről az épület legfelső szintjére. Az első nap maximum \(\displaystyle P\) darab lépcsőfokot tud lépni egy lépéssel. Mivel Balázs egy növekedésben levő tini, ezért a második nap már \(\displaystyle P+1\) fokot tud megtenni egy lépéssel, a harmadik nap \(\displaystyle P+2\) fokot, és így tovább. A legfelső szintről lefelé mindig lifttel közlekedik, csak felfelé lépcsőzik. Adjuk meg, hogy az \(\displaystyle M\) nap alatt legalább hány lépést tesz meg Balázs.

Bemenet: az első sor tartalmazza az \(\displaystyle N\), \(\displaystyle M\) és \(\displaystyle P\) számokat ebben a sorrendben.

Kimenet: adjuk meg a minimálisan megtett lépések számát.

Példa:

Bemenet	Kimenet
12 4 2	16

Korlátok: \(\displaystyle 1\le N,M,P\le {10}^{12}\). Időkorlát: 0,4 mp.

Értékelés: a pontok 50%-a kapható, ha \(\displaystyle N\le {10}^{3}\).

Beküldendő egy s141.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.

(10 pont)

statisztika