A KöMaL 2021. májusi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2021. június 15-én LEJÁRT. |
I. 538. A puzzle játék során lapokat kell ábrarészlet, illetve az oldalak illeszkedése alapján összerakni. Készítsünk programot i538 néven, amely egy \(\displaystyle N\times N\)-es puzzlet kirak az összekevert lapokból. A puzzle biztosan kirakható, a lapok mind rendelkezésre állnak és nem kell őket forgatni. A lapok 1-től \(\displaystyle N\times N\)-ig számozottak, és az oldalakat, ezzel az illeszkedést a szomszéd lapokhoz nem ismétlődő pozitív egész számok adják. Ha a lap egyik oldalán 0 érték szerepel, akkor az a puzzle szélén helyezkedik el.
A program standard bemenetének első sorában \(\displaystyle N\) (\(\displaystyle N\le 10\)), a sorok és oszlopok száma van. A következő \(\displaystyle N^2\) sorban, soronként 5 darab nemnegatív szám szerepel. Az első a lap sorszáma, a mintán a 3-as, majd felülről indulva az óramutató járásának megfelelően az oldalakat azonosító számok. Azokat a lapokat lehet összerakni, ahol az illesztendő oldalakon azonos szám szerepel.
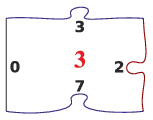
A program standard kimenetén szóközzel elválasztva a kirakott puzzle kártyáinak sorszáma szerepeljen sorfolytonosan.

Magyarázatul a kirakott puzzle:
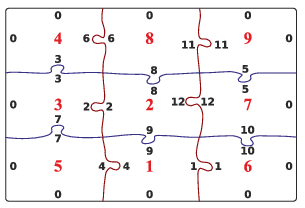
Beküldendő egy tömörített i538.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
I. 539. A Sudoku népszerűsége a sakkéval és a Rubik-kockáéval vetekszik. A Rubik-kockához hasonlóan sok változata van, a \(\displaystyle 4\times 4\)-es, a \(\displaystyle 9\times 9\)-es, a \(\displaystyle 16\times 16\)-os és az egynél több táblát összeillesztő láncolt feladatok. Ebben a feladatban a hagyományos \(\displaystyle 9\times 9\)-es Sudoku megoldásához készítünk némi segítséget. A Sudokuval már foglalkoztunk 2006 szeptemberében az I. 136. és 2007 novemberében az S. 29. számú feladatokban, de más aspektusokból.
Hozzuk létre táblázatkezelőben az i539 nevű munkafüzetet, abban pedig a Sudoku nevű munkalapot. Ezen állítsunk be 14 pt méretű Calibri típusú betűket és a megfelelő sormagasságot és oszlopszélességet, rajzoljuk meg a mintán látható szegélyeket és készítsük el a mintán látható táblázatokat.
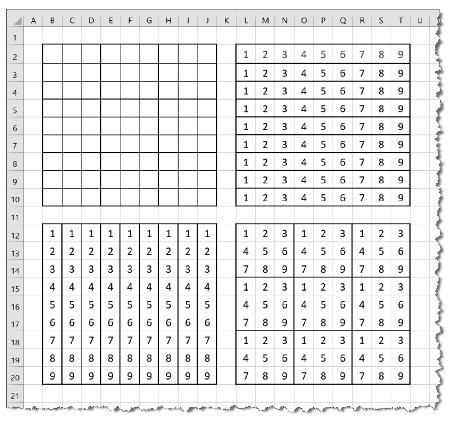
A négy szegélyezett terület közül a bal felsőbe kerül majd a Sudoku feladvány, a jobb felső, bal alsó és jobb alsó terület rendre azt fogja megmutatni, hogy az egyes sorokból, oszlopokból és szegmensekből melyik számjegyek hiányoznak még.
Keressünk a neten egy Sudoku feladványt, vagy gépeljük be az itt adott minta alapszámait. Az alapszámokat emeljük ki félkövér betűstílussal és halványszürke háttérszínnel.
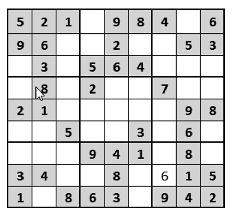
Gondoskodjunk arról, hogy a másik három területen csak azok a számok legyenek láthatók, amelyek az adott sorból, oszlopból vagy szegmensből hiányoznak.
Segítség a Sudoku kitöltésekor, ha egy számot kiválasztva a munkalap feltűnően megjeleníti a már beírt ilyen számokat, az egyes számjegyek darabszámát, továbbá azt, ha hibázunk a kitöltéskor, azaz olyan sorba vagy oszlopba írnánk be egy számjegyet, ahol ez a szám már szerepel. Mindezek érdekében hozzuk létre a következő mintán látható cellákat. A szükséges helyeken alkalmazzunk cellaegyesítést, eltérő betűméretet, egyéni számformátumot. Az X2 cella kitöltése legördülő lista segítségével történjen. A listában a számjegyek mellett szerepeljen a \(\displaystyle -\) (kivonás) jel.

A munkalapon csak a Sudoku nem alapszámot tartalmazó mezői és az X2 mező adatát lehessen megváltoztatni, lapvédelemre a komal szót használjuk jelszóként.
Ügyeljünk arra is, hogy a Z3:Z11 tartomány adatai akkor is helyes értékeket mutassanak, ha újabb számok kerülnek a Sudoku táblájába.
Feltételes formázással szabályozzuk, hogy az alábbi három ábra példáiban szereplő feliratok, színezések csak a megfelelő esetben, tehát szám kiválasztása, hiba vagy sikeres befejezés esetén jelenjenek meg.
Segédszámításokat az AB oszloptól kezdődően végezhetünk. A feladatban nem használható saját függvény vagy makró. A feladathoz tartozó három ábra a hátsó belső borítón található.
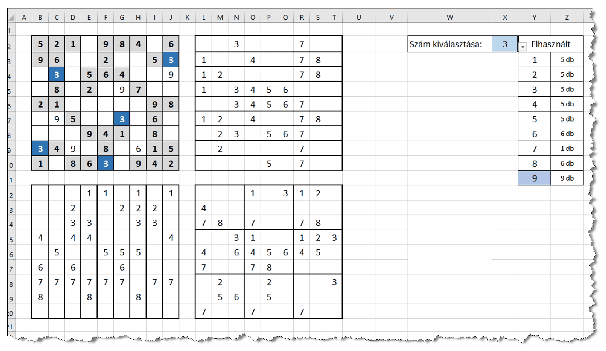


Beküldendő egy i539.zip tömörített mappában a táblázatkezelő munkafüzet és egy rövid dokumentáció, amelyben szerepel a megoldáshoz alkalmazott táblázatkezelő neve, verziószáma.
(10 pont)
I. 540. Lapunkban két cikk jelent meg önhasonló alakzatokról, azok tulajdonságairól, illetve az alakzatok LaTeX nyelven történő megrajzolásáról. Készítsük el a KöMaL logóra emlékeztető alábbi fraktált:
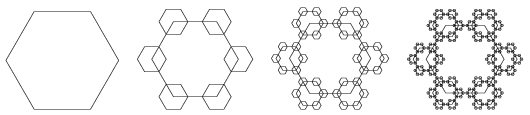
A cikkekben bemutatott Lindenmayer-rendszer segítségével dolgozzunk, a mintán az 1–4-edrendű ábrák szerepelnek.
Beküldendő a négy ábrát megrajzoló LaTeX forráskód.
(10 pont)
 |
I/S-jelű feladatokA beküldési határidő 2021. június 15-én LEJÁRT. |
I/S. 54. \(\displaystyle N\) darab gyöngyöt fűztek körbe nyakláncnak. Minden gyöngyszem vagy piros vagy kék. Egy lépésben kiválaszthatunk három szomszédos gyöngyöt és mindegyik színét az ellenkezőjére válthatjuk. Adjuk meg, hogy megoldható-e az, hogy az összes gyöngy ugyanolyan színű legyen.
Bemenet: az első sor tartalmazza az \(\displaystyle N\) számot. A következő sor tartalmaz \(\displaystyle N\) betűt, ami az egyes gyöngyszemeket írja le: P betű jelöl egy piros, K egy kék gyöngyöt. A szemeket körbe fűzték, tehát az első és utolsó gyöngyszemek szomszédok.
Kimenet: egyetlen sorba írjunk ki 1-et, ha lehetséges, -1-et ha nem lehetséges hogy minden gyöngyszem ugyanolyan színű legyen.
| Bemenet | Kimenet |
| 5 / PKPPK | 1 |
Egy lehetséges lépéssorozat: PKPPK – KPPPP – PKKPP – KKKKK.
Korlátok: \(\displaystyle 2\le N\le {10}^{5}\). Időkorlát: 0,3 mp.
Értékelés: a pontok 30%-a kapható, ha \(\displaystyle N\le 10\).
Beküldendő egy is54.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2021. június 15-én LEJÁRT. |
S. 153. Van egy derékszögű koordináta-rendszerünk, amelyben kezdetben három pont helyezkedik el. Egymás után újabb pontokat veszünk hozzá a ponthalmazhoz. Minden egyes új pont után szeretnénk tudni, mekkora a legkisebb területű konvex sokszög területe, mely minden eddig felvett pontot tartalmaz – a matematikusok ezt a sokszöget konvex buroknak nevezik. (Egy konvex sokszög tartalmaz egy pontot, ha a pont a sokszög belsejében, élén, vagy csúcsán helyezkedik el.)
Bemenet: Az első három sorban az eredeti három pont \(\displaystyle x\) és \(\displaystyle y\) koordinátái szerepelnek. A negyedik sorban az ezekhez hozzávett pontok \(\displaystyle N\) számát adjuk meg. A következő \(\displaystyle N\) sor mindegyike egy újonnan felvett pont \(\displaystyle x\) és \(\displaystyle y\) koordinátáit tartalmazza.
Kimenet: \(\displaystyle N\) sort kell kiírni, melyek mindegyike az \(\displaystyle i\)-edik pont hozzávétele utáni terület kétszeresét tartalmazza (ez mindig egész szám).
Példa:
| Bemenet (a / jel sortörést helyettesít) | Kimenet (a / jel sortörést helyettesít) |
| -1 -1 / 1 -1 / 1 1 / 2 / -1 1 / 2 2 | 8 / 12 |
Korlátok: \(\displaystyle 1\le N\le {10}^{5}\), \(\displaystyle -{10}^{8}\le xy\le {10}^{8}\), a koordináták egész számok, a kezdeti három pont nincs egy egyenesen. Időkorlát: 1 mp.
Értékelés: a pontok 30%-a kapható, ha \(\displaystyle N\le 100\).
Beküldendő egy s153.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.
