A KöMaL 2022. októberi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2022. november 15-én LEJÁRT. |
I. 571. Sokan szívesen játszanak a pozitív egész számokkal és azok számjegyeivel. Egy játékban a pozitív egészeket egyszerűsítjük több lépésben a következők szerint:
1. Az egyjegyű számokat nem egyszerűsítjük tovább.
2. A nem egyjegyű, de páros számú számjegyből álló számok esetén megvizsgáljuk, hogy a szám utolsó számjegye osztója-e a szám utolsó számjegyének elhagyásával keletkező számnak. Ha osztója, akkor a számot egyszerűsítjük arra számra, amelyet az utolsó számjegy elhagyásával kapunk.
3. A nem egyjegyű, de páratlan számú számjegyből álló számok esetén megvizsgáljuk, hogy a szám első számjegye osztója-e a szám első számjegyének elhagyásával keletkező számnak. Ha osztója, akkor a számot egyszerűsítjük arra számra, amelyet az első számjegy elhagyásával kapunk.
Készítsünk programot, amely megadja az \(\displaystyle [a;b]\) intervallumba eső (\(\displaystyle 10\le a < b \le 10\,000\,000\)) egyjegyű számra egyszerűsíthető pozitív egészek számát. A program a standard bemenet első sorából olvassa be a és b értékét, majd a standard kimenet első sorában adja meg a keresett egészek számát.
Példák:
| Bemenet | Kimenet |
| 20 80 | 15 |
| 10000 20000 | 415 |
| 1000000 3000000 | 7831 |
Beküldendő egy tömörített i571.zip állományban a program forráskódja, valamint a program rövid dokumentációja, amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
I. 572. Sok sportág lebonyolítási formája részben, vagy teljesen körmérkőzéses rendszerben történik. Az ilyen versenyek során minden résztvevő az összes többi résztvevővel egyszer megmérkőzik.
Készítsük el \(\displaystyle n=8\) résztvevőre a körmérkőzés párosításait táblázatkezelő alkalmazás segítségével a minta alapján. A mintán látható sárga mezőkbe szabad a csapatneveket begépelni, a többi cella értékét függvényekkel állítsuk elő. A megoldás annál több pontot ér, minél több a függvények között a másolható.
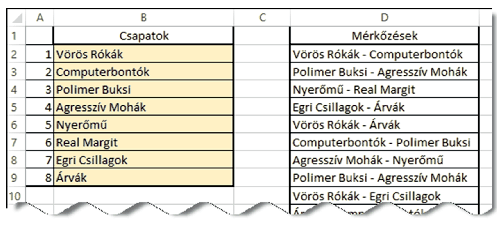
A táblázat szerkezetét, a cellák formázását állítsuk be a minta szerint. Ügyeljünk a megfelelő cellák szélességére, szegélyezésére és a tartalom igazítására. Segédszámításokat végezhetünk az E oszloptól jobbra, amelyek értelmezését feliratokkal segítsük elő vagy a dokumentációban írjuk le. A megoldásban saját függvény vagy makró nem használható.
Beküldendő egy tömörített i572.zip állományban a megoldást tartalmazó munkafüzet és a megoldás rövid leírását bemutató dokumentáció.
(10 pont)
I. 573. (É). Az atomok.txt egyszerű szöveges állomány az egyes atomok izotópjainak táblázatát tartalmazza. A táblázat minden sorában egy atom egy izotópjának adatai szerepelnek az alábbi minta szerint:
...
5 B 10 10,012 936 95(41) 0,199(7)
5 B 11 11,009 305 36(45) 0,801(7)
6 C 12 12,000 000 00(00) 0,9893(8)
6 C 13 13,003 354 835 07(23) 0,0107(8)
6 C 14 14,003 241 9884(40)
7 N 14 14,003 074 004 43(20) 0,996 36(20)
7 N 15 15,000 108 898 88(64) 0,003 64(20)
...
Az első szám az elem rendszáma (Z), a második a vegyjele (jelöljük V-vel), a harmadik az elem izotópjának tömegszáma (A), a negyedik szám az izotóp relatív atomtömege (m), az ötödik szám – amennyiben van – az izotóp előfordulásának aránya (jelöljük ea-val) egy adott elem esetén. A zárójelben lévő mennyiségek az értékek utolsó egy-két számjegyének hibáját jelentik, de a feladatban ezekkel nem kell számolni.
Készítsünk számítógépes programot, amely beolvassa a táblázatot tartalmazó szöveges állományt, majd megoldja az alábbi feladatokat. A képernyőre írást igénylő részfeladatok esetén – a mintához tartalmában hasonlóan – írjuk ki a képernyőre a feladat sorszámát (például: 2. feladat:), és utaljunk a kiírt tartalomra is. Ha a felhasználótól kérünk be adatot, akkor jelenítsük meg a képernyőn, hogy milyen értéket várunk. Mindkét esetben az ékezetmentes kiírás is elfogadott.
1. Olvassuk be az atomok.txt szöveges állományból az izotópok adatait. A zárójelben lévő mennyiségeket a számítás során nem fogjuk használni, így azokat nem kell eltárolni. Az egy sorban lévő értékek között szóköz az elválasztójel. Ügyeljünk arra, hogy a számok egész- és törtrésze között tizedesvessző szerepel, illetve a legtöbb esetben ezres tagolással vannak megadva az értékek, tehát itt is szóköz található. Amennyiben egy izotópnál az előfordulás aránya nincs megadva, úgy ott az ea értéket tekintsük nullának.
Helyes beolvasás esetén a fenti mintában szereplő izotópok számadatai feldolgozás után így néznek ki:
...
5 B 10 10.01293695 0.199
5 B 11 11.00930536 0.801
6 C 12 12.0 0.9893
6 C 13 13.003354835069999 0.0107
6 C 14 14.0032419884 0.0
7 N 14 14.00307400443 0.99636
7 N 15 15.00010889888 0.00364
...
(Az alkalmazott programozási nyelv számábrázolási pontosságától függően részben eltérő megoldások is születhetnek, például 6 C 14 14.003241988400001 0.0, ami szintén helyes.)
2. Kérjük be a felhasználótól egy elem vegyjelét, és írjuk ki az elem összes izotópjának adatait a következő formában:
2. feladat:
Kérem egy elem vegyjelét: C
Z=6 A=12 m=12.0 ea=0.9893
Z=6 A=13 m=13.003354835069999 ea=0.0107
Z=6 A=14 m=14.003241988400001 ea=0.0
3. Adjuk meg, hogy melyik elemeknek szerepel a táblázatban a legtöbb izotópjuk, és mennyi ez az érték.
3. feladat:
A legnagyobb izotópszám: 10
Az elemek: Sn
4. Készítsünk függvényt tomeg néven, amely megadja egy elem relatív atomtömegét figyelembe véve az izotópjainak relatív atomtömegét és előfordulások arányát.
A függvény bemenete az elem vegyjele, visszaadott értéke egy valós szám legyen. Például a szén (C) esetén az elem relatív atomtömege a három izotóp adatai alapján (lásd a mintát):
$$\begin{gather*} 12{,}0 \cdot 0{,}9893 + 13{,}003\,354\,835\,069\,999 \cdot 0{,}0107 + 14{,}003\,241\,988\,400\,001 \cdot 0{,}0 =\\ = 12{,}010\,735\,896\,735\,248. \end{gather*}$$5. Készítsünk tomegek.txt néven egyszerű szöveges állományt, amely azon elemek relatív atomtömegét tartalmazza, amelyeknél legalább egy izotóp aránya 0-tól különböző érték. Egy sorban egy elem vegyjele és relatív atomtömege szerepeljen. Az állományban minden megfelelő elem csak egyszer forduljon elő.
Minta a tomegek.txt állományról:
H 1.0077091323512934
He 4.002601932120928
Li 6.94003660291572
Be 9.012183065
B 10.811028046410001
C 12.010735896735248
N 14.006703211445798
Beküldendő egy tömörített i573.zip állományban a program forráskódja, valamint a program rövid dokumentációja, amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
Letölthető állomány: atomok.txt
(10 pont)
 |
I/S-jelű feladatokA beküldési határidő 2022. november 15-én LEJÁRT. |
I/S. 65. Adott egy \(\displaystyle N\) csúcsból és \(\displaystyle M\) élből álló irányítatlan gráf. A csúcsokat \(\displaystyle 1\)-től \(\displaystyle N\)-ig indexeljük. A gráfot az alábbi módon több lépésben bővítjük élek hozzáadásával: egy lépésben keresünk egy olyan \(\displaystyle x\) és \(\displaystyle y\) csúcspárt, amely nincs összekötve, de létezik olyan \(\displaystyle z\) csúcs, ami össze van kötve \(\displaystyle x\)-szel és \(\displaystyle y\)-nal is (\(\displaystyle 1\le x,y,z\le N\)). Ha találtunk ilyen \(\displaystyle x, y\) csúcspárt, akkor összekötjük őket egy éllel, ha nem, akkor befejeződött a gráf bővítése.
Adjuk meg, hogy a gráfbővítés befejeztével hány él van a gráfban. Mivel ez a szám nagyon nagy is lehet, ezért a szám \(\displaystyle (10^{9}+7)\)-tel vett osztási maradékát kell megadni.
A standard bemenet első sorában az \(\displaystyle N\) és \(\displaystyle M\) számok szerepelnek szóközzel elválasztva. A további \(\displaystyle M\) sor mindegyike 2 számot tartalmaz szóközzel elválasztva: egy adott él két végpontjának indexét.
A standard kimenet egyetlen sorában egy szám szerepeljen: a gráfbővítés befejeztével a gráfban levő élek száma modulo \(\displaystyle 10^{9}+7\).
| Bemenet (a / jel sortörést helyettesít) | Kimenet |
| 8 5 / 1 2 / 2 4 / 3 2 / 6 7 / 7 8 | 9 |
Korlátok: \(\displaystyle 2 \le N,M \le 10^{5}\). Időlimit: 0,4 mp.
Értékelés: a pontok 50%-a kapható, ha a program az \(\displaystyle N,M \le 500\) tesztesetekre helyes kimenetet ad.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2022. november 15-én LEJÁRT. |
S. 164. A fordítóprogramok nagyon alacsony szinten átrendezhetik a forrásprogramban kiszámítandó kifejezésben az elvégzendő műveletek sorrendjét azért, hogy időt vagy memóriát spóroljanak. Ez sokat javíthat egy programon, de nem változtathatja meg annak jelentését. Ebben a feladatban egy egyszerű számítás memóriaigényét próbáljuk csökkenteni.
Adott egy csak változókat, valamint összeadás és szorzás műveleteket tartalmazó kifejezés. Az egyszerűség kedvéért fordított lengyel jelölést használunk. Például az \(\displaystyle (a+b)*c\) kifejezés lengyel formában \(\displaystyle ab+c*{}\) lesz. Ennek előnye, hogy a számítógép ezt balról jobbra haladva egyszerűen végre tudja hajtani. Kezdetben az összes változó értéke bent van a memóriában, mindegyik egy egységnyi tárhelyet foglal el. Egy matematikai művelet végrehajtása után az eredmény egy új (egységnyi) memóriaterületre kerül. Az előző példában \(\displaystyle x=a+b\), \(\displaystyle y=x*c\). A program így 5 egységnyi memóriát használ, kezdetben \(\displaystyle a\), \(\displaystyle b\) és \(\displaystyle c\) értékének, majd \(\displaystyle x\) és \(\displaystyle y\) tárolására.
A kifejezés kiértékelése javítható, ha a később már nem használt (egységnyi) memóriaterületeket minden lehetséges alkalommal felülírjuk. A példa egy lehetséges végrehajtása ezzel a javítással: \(\displaystyle a=a+b\), \(\displaystyle b=a*c\). A program így 3 egységnyi memóriát használ a kezdeti változók miatt. (Nem számít, hogy az eredmény végül melyik változóba kerül.)
Készítsünk programot, amely egy lengyelformában adott kifejezés esetén megadja, hogy hány egységnyi tárhely szükséges a kifejezés kiértékeléséhez az eredeti és az optimalizált módszer felhasználásával.
A bemenet első és egyetlen sora egy számítást tartalmaz a fordított lengyel jelölés szerint. Ennek minden karaktere az angol abc egy kisbetűje, illetve a ,,+'' és ,,*'' karakter lehet.
A kimenet első sorába a számolás optimalizáció nélküli, a második sorába az optimalizáció utáni memóriaigényét kell írni.
Minta:
| Bemenet | Kimenet (a / jel sortörést helyettesít) |
| ab+bc+*ca+* | 8 / 4 |
Időlimit: 0,5 mp.
Értékelés: a pontok 20%-a kapható, ha a megoldás a kimenet első sorát helyesen határozza meg.
Beküldendő egy s164.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

