| [258] jenei.attila | 2006-11-08 16:24:57 |
 Kedves Ákos!
Azt értem amit írsz (valószínűleg az A-tól van az M AC/3 távolságra), de innen még szerintem igen messze van a megoldás (legalábbis én nem látom). Ha van türelmed, légyszíves írd le részletesebben. Köszi.
Az én megoldásom vázlatosan: Az A csúcsból b,c,d vektorokat irányítunk a B,C,D csúcsokhoz. Ekkor az A'-ből B',C',D' csúcsokhoz mutató vektorok: b'=2c-3b, c'=2d-2b-c, d'=-2b-d. A tetraéder térfogata az egy csúcsból induló élvektorok vegyes szorzatának 6-oda. A b'c'd' vegyes szorzatot képezve (felhasználva a skaláris és vektoriális szorzás vektor összeadásra nézve disztributív tulajdonságát és a konstans eh.-tók "kiemelhetőségét"), -8cdb+4cbd-3bcd=15cbd kapunk (itt a vektorok egymás után írása a vegyes szorzatukat jelenti), vagyis a tetraéderünk térfogata valóban 15-szörösére nőtt.
|
| Előzmény: [254] S.Ákos, 2006-11-07 20:13:34 |
|
|
|
|
|
| [253] jenei.attila | 2006-11-06 11:25:32 |
 A B.3927 feladat megoldása, ha már így tették fel a kérdést, gondolom 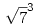 . Érdekelne a feladat teljes megoldása. . Érdekelne a feladat teljes megoldása.
|
|
| [252] jenei.attila | 2006-11-06 11:21:25 |
 Érdekesebb a B.3923 feladat. Az nxn-es sakktáblán 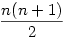 átló húzható be, vagyis az igazi sakktáblán 36. Itt a megoldás alapja az, hogy a mezőket elválasztó egyenesek metszéspontjaiból (csomópontok) legfeljebb egy-egy átló húzható. Tekintsük az nxn-es tábla két felső sorából, és két bal oldali oszlopából álló "karéjt". Ebben a belső csomópontok száma n+(n-1), azaz a karéjban legfeljebb ennyi átló húzható be. Ennyi azonban be is húzható, ha a karéj "külső" sávjában húzzuk az átlókat É-Ny,D-K irányban. A Megmaradt (n-2)x(n-2)-es táblában a két sáv széles karéjban (n-2)+(n-3) átló húzhat, s.í.t. Vagyis összesen legfeljebb n+(n-1)+...+1= átló húzható be, vagyis az igazi sakktáblán 36. Itt a megoldás alapja az, hogy a mezőket elválasztó egyenesek metszéspontjaiból (csomópontok) legfeljebb egy-egy átló húzható. Tekintsük az nxn-es tábla két felső sorából, és két bal oldali oszlopából álló "karéjt". Ebben a belső csomópontok száma n+(n-1), azaz a karéjban legfeljebb ennyi átló húzható be. Ennyi azonban be is húzható, ha a karéj "külső" sávjában húzzuk az átlókat É-Ny,D-K irányban. A Megmaradt (n-2)x(n-2)-es táblában a két sáv széles karéjban (n-2)+(n-3) átló húzhat, s.í.t. Vagyis összesen legfeljebb n+(n-1)+...+1=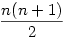 átló húzható be. átló húzható be.
Más megoldás?
|
|
| [251] jenei.attila | 2006-11-06 10:59:35 |
 A B.3931 feladat szerintem nagyon könnyű, nem tudom miért ér 5 pontot. A 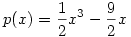 polinom egy lehetséges megoldás. polinom egy lehetséges megoldás.
|
|
| [250] V Laci | 2006-10-28 23:16:06 |
 Az én megoldásom vázlatosan a B.3928-ra:
Először is lássuk be, hogy egy tetszőleges ABCD téglalapra és egy O pontra teljesül az OA2+OC2=OB2+OD2. Ennek bizonyítása Pitagorasz-tétel segítségével könnyen megtehető.
Ez teljesülni fog a feladatbeli PAQB téglalapra és az O középpontra. Így r2+r2=OP2+OQ2. Innen adódik, hogy OQ2=2r2-OP2, és mivel az OP távolság nem változik a köbeforgatás során, az OQ értéke állandó, vagyis a Q egy O középpontú 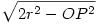 körpályán fog mozogni. körpályán fog mozogni.
|
| Előzmény: [249] jenei.attila, 2006-10-28 18:38:31 |
|
| [249] jenei.attila | 2006-10-28 18:38:31 |
 A B.3928 is egy érdekes feladat, egy "geometriai" bizonyítást szeretnék rá látni. Az én megoldásom:
Az adott kör középpontja legyen O, az O-ból induló, feladatban szereplő pontokhoz húzott helyvektorok: a,b,p,q. Ekkor q=a+b-p, és a feltétel szerint (PA merőleges PB-re) (a-p)(b-p)=0 (skaláris szorzás). Emeljük q-t skalárisan négyzetre:
q2=a2+b2-p2+2(a-p)(b-p)=2r2-p2
Itt r a kör sugara, vagyis a q vektor hossza csak a kör sugarától és a P pont O-tól való távolságától függ. Vagyis a keresett mértani hely egy O középpontú 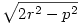 sugarú kör. sugarú kör.
|
|
| [248] jenei.attila | 2006-10-26 12:44:56 |
 A B.3926 feladat egy lehetséges megoldása:
Annának van nyerő stratégiája, mert mindig páros sok 1 kavicsot tartalmazó, és páros sok páros számú kavicsot tartalmazó kupacot tud hagyni az ellenfelének. Balázs ezt az állapotot bármit lép is, mindig elrontja, Anna pedig újra ezt az állapotot tudja előidézni. A végállapot (elfogyott a kavics) is ide tartozik, vagyis Anna nyer ha jól játszik.
Esetleg más megoldás?
|
|
|
|
|
| [244] jenei.attila | 2006-10-24 14:57:50 |
 A B.3929 feladat megoldására lennék kíváncsi. Az én megoldásom:
x=100i+1/10, y=25j+12/10, z=100k+9/10 ahol i,j,k tetszőleges természetes számok.
|
|
| [243] rizsesz | 2006-07-26 13:43:53 |
 hát, simán elképzelhetőnek tartom, hogy több és kimagaslóan jobb diák van. még régebben volt a kezemben egy abacus, amiben emlékszem, hogy zrínyi megoldásokat mutattak be, és az volt a lényeg, hogy a 6. osztályosok a közös feladatokon folyamatosan jobban teljesítettek, mint a 7.-esek. ti vagytok az akkori 6. évfolyam. amúgy emellett most a 9. évfolyamról van diákolimpikon is, illetve ehhez kapcsolódóan az a-ban nyújtott teljesítményre is felhívnám a figyelmet.
persze a kömal, illetve az abacus alapján ezt nem lehet eldönteni, de azért elég valószínűnek tartom, hogy a kilencedikesek jobbak.
|
|
| [242] sakkmath | 2006-07-26 13:33:17 |
 Tisztelt feladatjavítók! A B.3896.-tal kapcsolatban két kérdésem van: 1. Volt-e olyan beküldött megoldás, amely azt a jogos feltevést használta ki, hogy a keletkezett ikerháromszögek bármelyike nyújtva tükrözéssel az eredeti háromszögbe vihető? Feltehető, hogy az ilyen, transzformáción alapuló, tisztán elemi geometriai megoldás elegánsabb, mint a honlapon vázolt koordinátarendszeres módszer. 2. A feladat 4 pontot ért, de a megoldást beküldők számára nehezebb lehetett mint sok 5-pontos, legalábbis a közölt statisztika ezt mutatja. Nem lett volna reálisabb inkább 5 pontot adni rá? Üdvözlettel: a feladat szerzője
|
|
|
| [240] Csimby | 2006-07-26 00:35:48 |
 Szia!
Négyzetre emelés és rendezés után már lehet közepezni (persze nem biztos, hogy megéri).
(1) 6x2y2 x4+y4+(x2+y2)2xy x4+y4+(x2+y2)2xy
Innen például:
2x2y2 x4+y4 x4+y4
Ez a számtani-mértaniból jön ki, a következő pedig a mértani és négyzetesből:
2xy x2+y2 x2+y2
Ebből pedig:
4x2y2 (x2+y2)2xy (x2+y2)2xy
A két egyenlőtlenséget összeadva kapjuk a bizonyítandó állítást. Másik lehetőség, ha (1)-ben leosztaszt x2y2-tel, ekkor a pozitív a-kra érvényes 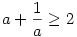 állítás (ami a számtani-mértani közepek közti egyenlőtlenség egyszerű következménye) többszöri felhasználásából is adódik az állítás. állítás (ami a számtani-mértani közepek közti egyenlőtlenség egyszerű következménye) többszöri felhasználásából is adódik az állítás.
Nem nagyon jut eszembe olyan dolgozat ahol valaki a négyzetreemelés előtt közepezett volna. De csak az elektronikusan beküldött dogákat tudtam újra átnézni, szóval lehet hogy papíron volt olyan megoldás is.
Csimby
|
| Előzmény: [239] ScarMan, 2006-07-15 18:33:53 |
|
| [239] ScarMan | 2006-07-15 18:33:53 |
 A B.3916-os feladatra van 'közepes' megoldása valakinek? Maga a feladat adja az ilyen becsléseket, de én minden ilyen értelmesnek tűnő próbálkozással túlbecsültem, és maradt egy sima négyzetreemeléses-rendezéses megoldás. Feltételezem hogy nem csak félrevezetésként szerepel a feladatban 4 közép :)
|
|
| [238] lorantfy | 2006-07-11 13:01:33 |
 Szia Jónás!
Hát ez az! A megoldás végülis az lenne, hogy belássuk, k db fej esetén a dobássorozatok száma 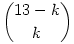 , ebből aztán bárki kiszámolja az esetek összegét. , ebből aztán bárki kiszámolja az esetek összegét.
Aki nem tudta megoldani az viszont a közölt megoldásból nem ért semmit.
Tehát arról van szó, hogy mivel két fej nem állhat egymás mellet, ha egy adott dobássorozatban balról jobbra haladunk, minden fejet írásnak kell követnie. Kivéve az utolsó dobásnál álló fejet, ha éppen fej áll ott.
A 13. helyre odaírunk egy fix I-t. Igy biztosak lehetünk benne, hogy minden F-et I követ.
Tegyük fel, hogy k db F van a sorozatban. Most az FI párokat egy új elemnek tekintve, k db I-t eltüntettünt, tehát (13-k) db (I vagy FI) elemünk maradt, tehát (13-k) elem közül kell k elemet kiválasztanunk.
|
 |
| Előzmény: [236] jonas, 2006-07-08 12:09:04 |
|
| [237] Yegreg | 2006-07-08 20:16:26 |
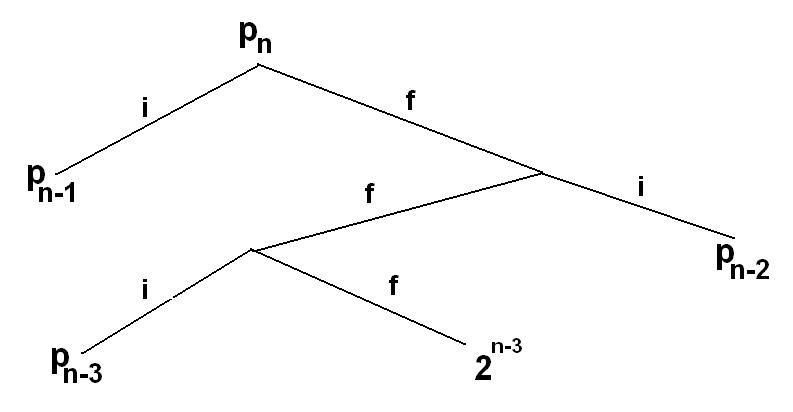
 Leírom az analóg B feladatra a megoldásom, mert ez könnyen általánosítható, és egyszerű rekurzióra vezeti vissza őket.
Jelölje pn azt, hogy n dobásból hány esetben szerepelhet a leírt eredmények között 3 egymást követő fej! Ha egy adott n-nél dobunk egyet, akkor, ha az írás, akkor ez nem lehet része fejhármasnak, tehát az innen létrejövő lehetőségek száma pn-1 hiszen az egymást követő fejek szempontjából olyan, mintha itt újat kezdenénk, csak eggyel kevesebb dobással. Ha az első dobás fej, a második írás, akkor hasonlóan ahhoz, hogy az első írás, ez további pn-2 féle lehetőséget jelent, mivel itt is olyan, mintha újat kezdenénk, csak már 2-vel kevesebb dobással. Ha az első és a második dobás is fej, és a harmadik írás, akkor az első írás és második írás esethez analóg módon itt további pn-3-féle lehetőség van. Fa az első három dobás fej, akkor a dobások között már bizonyosan van 3 fej, tehát a többi kimenete tetszőleges, azaz a a további n-3 dobás mindegyi fej vagy írás is lehet, tehát még 2n-3 lehetőség van.
Az összes lehetőség ezen diszjunkt alesetek összege lesz, azaz
| pn=pn-1+pn-2+pn-3+2n-3 | (1) |
Nyilván 0, 1 és 2 dobásból nem lehet egy esetben sem 3 fej, tehát p0=p1=p2=0, azonban innen már látható, hogy az egész feladat egy kissé módosított 3-as Fibonacci-sorozat kiszámolására redukálódik. Tehát: (az (1) egyenletbe egyből helyettesítve)
p3=0+0+0+20=1
p4=0+0+1+21=3
p5=0+1+3+22=8
p6=1+3+8+23=20
p7=3+8+16+24=47
p8=8+20+47+25=107
p9=20+47+107+26=238
p10=47+107+238+27=520
p11=107+238+520+28=1121
p12=238+520+1121+29=2391
Azon esetk száma tehát, ahol van 3 egymást követő fej 12 dobás esetén 2391. Nyilván összesen 212=4096-féle eset lehetséges a dobássorozat kimeneteleként, hiszen minden dobás 2-féle lehet, tehát a 3 egymást követő fej nélküli esetek száma 4096-2391=1705. A valószínűség tehát:
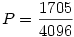
|
 |
|
| [236] jonas | 2006-07-08 12:09:04 |
 Nézzük. Ha k fejet és 12-k írást kell elhelyezni úgy, hogy nincs két szomszédos fej, akkor 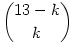 lehetőség van, amit úgy kaphatunk meg, hogy k darab FI és 13-2k darab I sorozatot rakunk tetszőleges sorrendbe, összefűzzük, és levágjuk a záró I-t. Ezt összegzi a megoldás, de tényleg hozzáfűzhettek volna több magyarázatot, mert aki ezt a trükköt nem ismeri, annak talán nem világos. lehetőség van, amit úgy kaphatunk meg, hogy k darab FI és 13-2k darab I sorozatot rakunk tetszőleges sorrendbe, összefűzzük, és levágjuk a záró I-t. Ezt összegzi a megoldás, de tényleg hozzáfűzhettek volna több magyarázatot, mert aki ezt a trükköt nem ismeri, annak talán nem világos.
Egyébként ez a feladat is megoldható brute force módon, mégpedig elég egyszerűen, mert csak 4096 sorozatot kell kipróbálni. Abból is 337 jön ki (a 12+2-edik fibonacci-szám, nem véletlenül).
|
| Előzmény: [235] jonas, 2006-07-08 11:24:28 |
|
|
| [234] lorantfy | 2006-07-07 15:17:46 |
 Kedves KöMaL Megoldók!
Aki érti a C. 851. feladat hivatalos megoldását és van egy kis ideje legyen szíves nekem szemléletesen elmagyarázni! (0 és 1 fej esete OK!)
|
|





 +1)(2
+1)(2 3 egészre
3 egészre

 x4+y4+(x2+y2)2xy
x4+y4+(x2+y2)2xy




