| [190] Hajba Károly | 2004-11-24 14:47:40 |
 Kedves Svejk!
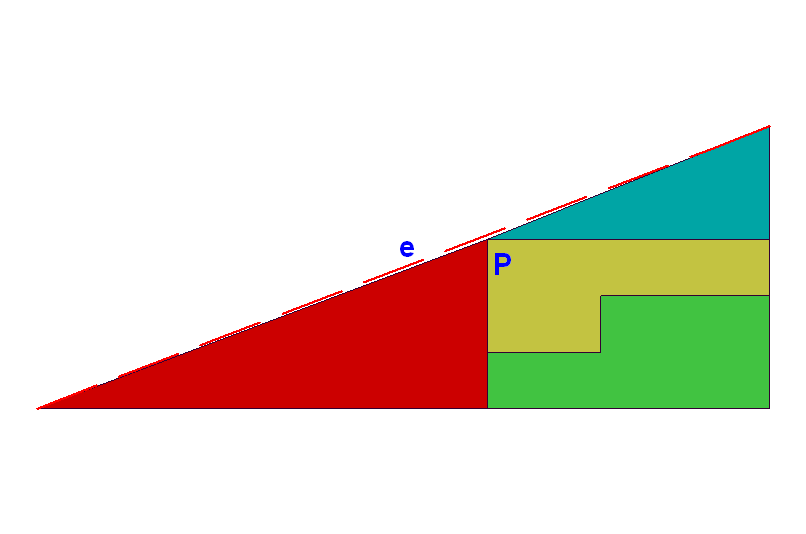
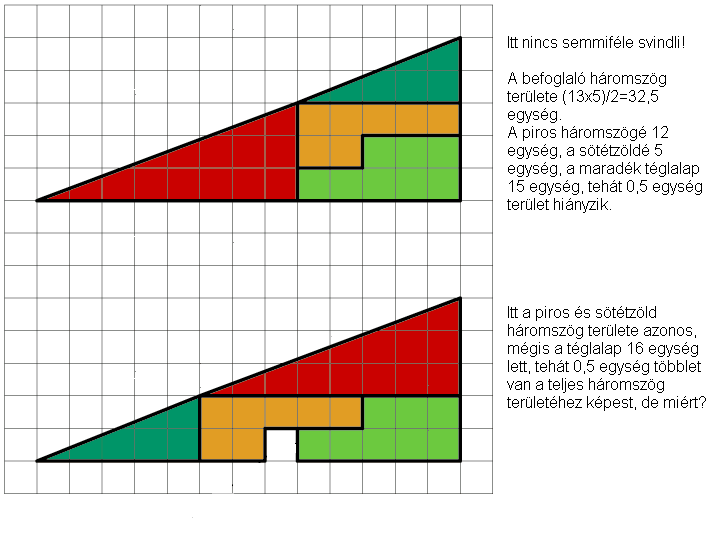
Félrevezető a vastag keret. Átrajzoltam vékonnyal és behúztam az igazi átfogót.
Cserébe mondd meg nekünk, hogy mennyi a P töréspont és e átfogó közötti távolság, ha a háromszög két befogója 13 és 5 egység.
HK
|
 |
| Előzmény: [187] svejk, 2004-11-24 13:22:42 |
|
|
| [188] jenei.attila | 2004-11-24 13:23:21 |
 Az a baj, hogy a befoglaló "háromszög" nem háromszög, csak majdnem. Ugyanis ha az lenne, akkor a piros és a sötétzöld háromszögeknek hasonlóaknak kellene lenni, de nem azok (2/5 nem = 5/8).
|
| Előzmény: [186] svejk, 2004-11-24 13:15:02 |
|
| [187] svejk | 2004-11-24 13:22:42 |
 Kedves Matekosok!
Elnézést, hogy előbb a képet küldtem.:( Úgy tudom, hogy ez egy elég régi feladvány, de még senkitől nem kaptam kielégítő magyarázatot, hogy miért változnak meg a részterületek összegei. Help!
A választ előre is köszönöm!
|
|
|
| [185] Kós Géza | 2004-11-22 16:34:40 |
 Kedves Géza,
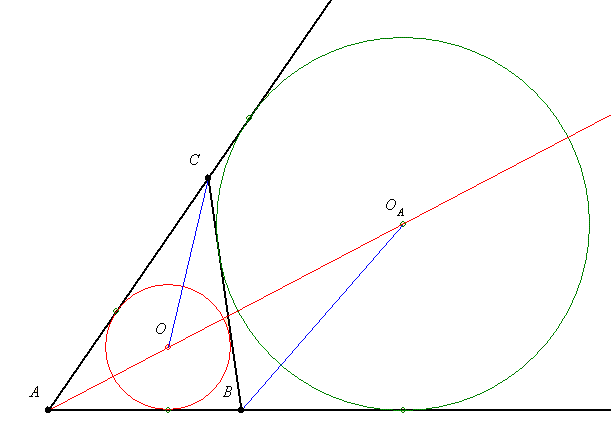
Ezek szerint a kívülről érintő körökre gondoltál.
Invertáljuk a beírt kört és a BC egyenest az A középpontú, 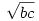 sugarú körre, majd mindkettőt tükrözzük az A-ból induló szögfelelezőre. A B és C pont képe önmaga, a BC egyenes képe a körülírt kör, a beírt kör képe pedig az AB és AC félegyeneseket, valamint a körülírt kört érintő kör, vagyis kbc. sugarú körre, majd mindkettőt tükrözzük az A-ból induló szögfelelezőre. A B és C pont képe önmaga, a BC egyenes képe a körülírt kör, a beírt kör képe pedig az AB és AC félegyeneseket, valamint a körülírt kört érintő kör, vagyis kbc.
A beírt körnek az AB, AC félegyeneseken levő érintési pontjai az A ponttól s-a távolságra vannak. A kbc kör érintési pontjai ennek megfelelően 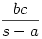 távolságra vannak A-tól. A sugarak aránya ugyanaz, mint az érintő szakaszoké, tehát távolságra vannak A-tól. A sugarak aránya ugyanaz, mint az érintő szakaszoké, tehát
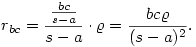
Mindhárom körre felírva és összeszorozva,
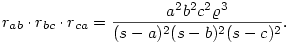
Beírva a Héron-képletet és a 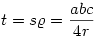 területképleteket, területképleteket,
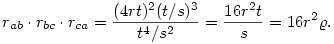
|
| Előzmény: [184] BohnerGéza, 2004-11-19 14:22:11 |
|
|
| [183] Kós Géza | 2004-11-17 18:12:11 |
 Nekem az jött ki, hogy ha a három kör kívülről érinti a körülírt kört, akkor
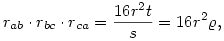
és a szorzatot nem lehet csak r-rel és s-sel kifejezni, de ki lehet fejezni a beírt és körülírt kör sugarával.
Ha a három kör belülről érinti a körülírt kört, akkor
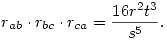
|
| Előzmény: [182] BohnerGéza, 2004-11-17 09:35:09 |
|
| [182] BohnerGéza | 2004-11-17 09:35:09 |
 45. feladat: A r-ca jelentse az ABC háromszög körülírt körét, valamint az AB és BC - ilyen irányú - félegyeneseket érintő kör sugarát. Mennyi az r-ca, r-ab és r-bc szorzata a körülírt kör r sugarával és az s félkerülettel kifejezve?
|
|
|
| [180] lorantfy | 2004-11-10 20:31:38 |
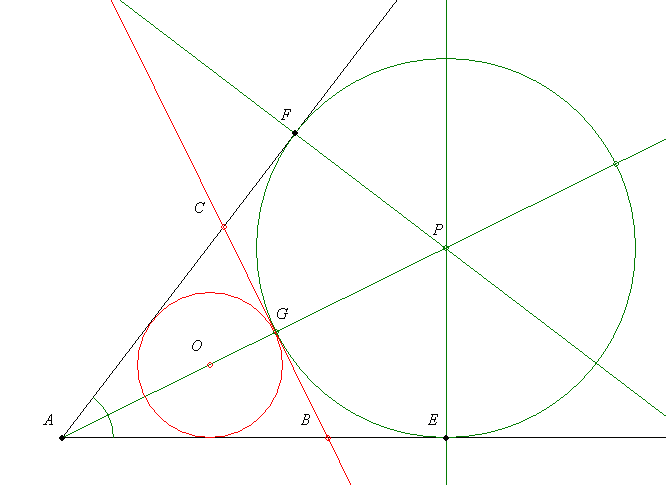
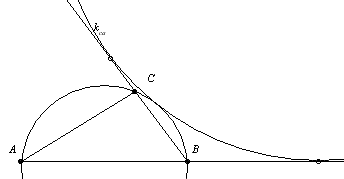
 44. feladat megoldása: Vegyük fel az  szöget és mérjük fel a száraira a félkerületet. A kapott E és F pontban állítsunk merőlegest. Ezek metszéspontja P a háromszög kívülírt körének középpontja, sugara ra=PE. Rajzoljuk meg a kört! Az a oldal ennek a körnek érintője. Húzzuk meg az AP szögfelezőt, ez a kört a G pontban metszi. szöget és mérjük fel a száraira a félkerületet. A kapott E és F pontban állítsunk merőlegest. Ezek metszéspontja P a háromszög kívülírt körének középpontja, sugara ra=PE. Rajzoljuk meg a kört! Az a oldal ennek a körnek érintője. Húzzuk meg az AP szögfelezőt, ez a kört a G pontban metszi.
A háromszög területe T= s. Mivel s adott, ez akkor a legnagyobb, ha a beírt kör a lehető legnagyobb. Ez pedig akkor van ha a beírt kör G pontban érinti a kívülírt kört. s. Mivel s adott, ez akkor a legnagyobb, ha a beírt kör a lehető legnagyobb. Ez pedig akkor van ha a beírt kör G pontban érinti a kívülírt kört.
Tehát a maximális területű háromszög egyenlő szárú.
Így a szerkesztés befejezése egyszerű: Állítsunk merőlegest a G pontban a szögfelezőre, ez lesz az a oldal.
|
 |
| Előzmény: [177] BohnerGéza, 2004-11-09 10:36:42 |
|
|
| [178] BohnerGéza | 2004-11-09 13:29:57 |
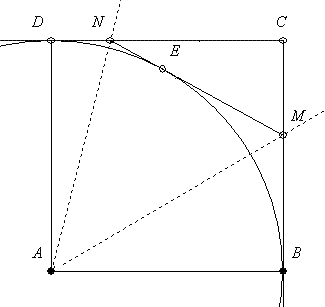
 A B.3736. feladat és egy megoldása: Az egységnyi oldalú ABCD négyzet CD oldalán adott az N, CB oldalán pedig az M pont úgy, hogy az MCN háromszög kerülete 2. Mekkora az MAN szög?
Adott az MCN háromszög egy szöge (derékszög) és kerülete, ami kettő. Így félkerülete s=1. Tudjuk, hogy a csúcsból a szemközti hozzáírt körig húzott érintőszakasz hossza s, így esetünkben a C-vel szemközti érintőkör B-nél ill. D-nél érinti a C-ből induló oldalakat, tehát középpontja A. Az AM és AN az MCN külső szögfelezői. Tükrözve AM-re B-t a E-t, majd AN-re E-t a D-t kapjuk. A két tengelyes tükrözés B-t A körül 90 fokkal forgatta el, így a két tengely szöge 45 fok.
|
 |
|
| [177] BohnerGéza | 2004-11-09 10:36:42 |
 44. feladat: . Szerkesztendő a lehető legnagyobb területű háromszög, ha adott egy szöge és a kerülete!
|
|
| [176] matekos04 | 2004-11-08 19:54:26 |
 Udv. mindenkinek!
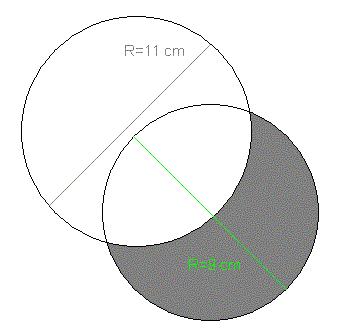
Maglattam ezt a topikot erdekesnek talaltam es gondoltam hogy bekuldök egy feladatot:
A kerdesem az hogy hany negyzetcentimeter a szurke terulet.
|
 |
|
|
| [174] lorantfy | 2004-10-24 11:21:22 |
 Kedves Géza!
A 42. feladatra egy látványosabb bizonyítást szerettem volna adni, de idő hiányában beérem azzal, hogy visszavezetem egy ismert összefüggésre. Hivatkozok - és egyben felhívom a figyelmeteket - Kiss György: Amit jó tudni a háromszögekről című cikkére itt.
42. feladat megoldása:
Bizonyítandó: 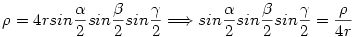
Felhasználjuk, hogy 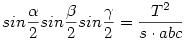
Tehát, be kell látnunk, hogy 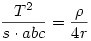 Átszorozva: Átszorozva: 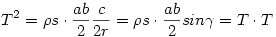
|
| Előzmény: [172] BohnerGéza, 2004-10-21 09:01:05 |
|
|
| [172] BohnerGéza | 2004-10-21 09:01:05 |
 41. feladat: Az ABC háromszög szokásos jelölései mellett (O a beírt, Oa az A-val szemközti hozzáírt kör középpontja) igazoljuk, hogy AO*AOa = b*c.
42. feladat: ( ró a beírt kör, r a körülírt kör sugara ) bizonyítandó, hogy
ró = 4r*sin(alfa/2)*sin(béta/2)*sin(gamma/2)
|
|
|
| [170] BohnerGéza | 2004-10-14 22:50:38 |
 40. feladat: Az ABC háromszög és a k-val jelölt kör feleljen meg a 37. feladatban ( [169.] hozzászólásban ) leírtaknak. Igazoljuk, hogy ABC magasságpontja k-n van! ( pontosítható az állítás )
Ez a feladat ötletet adhat a 37. feladat megoldásához, illetve segíthet a [169.] hozzászólásban vázolt számolásban.
|
| Előzmény: [158] BohnerGéza, 2004-09-08 20:25:06 |
|
| [169] BohnerGéza | 2004-10-11 15:47:59 |
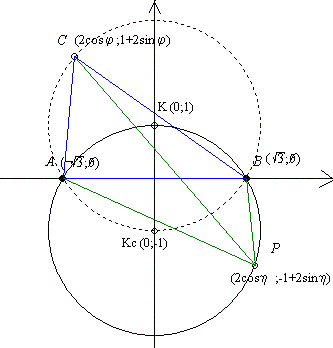
 A 37. feladat: megoldásához. Egyelőre nincs jobb ötletem, mint a koordináta geometriai út, ez járható is. A mellékelt ábrán használt jelöléseket ajánlom. ( Hasonlóság miatt elég az ott látott AB szakasz esetén bizonyítani. ) A 38. feladat alapján először az APB és az ABC háromszög Euler-egyenese metszéspontjának meghatározását ajánlom. Szép, érdekes eredményt kapunk. Néhány nap múlva ezt közlöm.
|
 |
| Előzmény: [159] BohnerGéza, 2004-09-13 08:51:57 |
|
|
| [167] newbee | 2004-10-01 17:28:05 |
 Sziasztok!
bocs a zavarasert, pici segitseget szeretnek kerni affin transzformacikkal kapcsolatban. Eleg volna egy link is, ahol esetleg elmagyarazzak hogyan kell megszerkeszteni, de az is, ha cimszavakban elmeselitek.
Olyant kellene csinalnom, hogy adott egy haromszog, az affinitas iranya parhuzamos a tengellyel, es az egymasnak megfelelo pontok egy oldalra kerulnek. A masik: ugyanezen haromszog ferde affin kepe. A tengely nem metszi a haromszoget, es az egymasnak megfelelo pontok egy oldalon vannak.
Koszi :)
|
|
| [166] Hraskó András | 2004-09-29 03:16:57 |
 A legfrissebb Kömalban olvasható egy-egy szép megoldás a B.3678. és a B.3680. feladatra. Mind a két feladatra adható frappáns projektív geometriai gondolatmenet, amivel pld az utóbbi feladat állítását messzemenően általánosítani is lehet. Talán a PÁLYÁZAT-on is sikerrel indulhat az, aki megtalálja ezeket a megoldásokat.
|
|









 =40
=40 szöget és mérjük fel a száraira a félkerületet. A kapott E és F pontban állítsunk merőlegest. Ezek metszéspontja P a háromszög kívülírt körének középpontja, sugara ra=PE. Rajzoljuk meg a kört! Az a oldal ennek a körnek érintője. Húzzuk meg az AP szögfelezőt, ez a kört a G pontban metszi.
szöget és mérjük fel a száraira a félkerületet. A kapott E és F pontban állítsunk merőlegest. Ezek metszéspontja P a háromszög kívülírt körének középpontja, sugara ra=PE. Rajzoljuk meg a kört! Az a oldal ennek a körnek érintője. Húzzuk meg az AP szögfelezőt, ez a kört a G pontban metszi.  s. Mivel s adott, ez akkor a legnagyobb, ha a beírt kör a lehető legnagyobb. Ez pedig akkor van ha a beírt kör G pontban érinti a kívülírt kört.
s. Mivel s adott, ez akkor a legnagyobb, ha a beírt kör a lehető legnagyobb. Ez pedig akkor van ha a beírt kör G pontban érinti a kívülírt kört. 





 hasonló ABOA
hasonló ABOA