| [232] BohnerGergő | 2005-05-05 19:28:02 |
 Kiegészítés az 53. feladat megoldásához:
Az indoklásból kimaradt, hogy a két forgatás szorzata azért egyenlő az F körüli 180 fokos forgatással, mert a két forgatás szögének összege 180 fok.
|
| Előzmény: [231] BohnerGergő, 2005-05-05 19:03:13 |
|
| [231] BohnerGergő | 2005-05-05 19:03:13 |
 D-nél a szög delta, E-nél epszilon. Tudjuk: epszilon=180-delta Az egyenlőszárú háromszögek miatt, ha A-t forgatjuk E körül epszilonnal, majd D körül deltával akkor B-t kapjuk. Ugyanígy A-ból B-t kapjuk ha középpontosan tükrözzük F-re. Egy forgatás két tengelyes tükrözés szorzata, még pedig akkor, ha a tengelyek szöge fele a forgatás szögének. Vegyük fel a 3 tükörtengelyt az ábrán látható módon. Ekkor: DEF szög 90-(delta/2) és EDF szög delta/2. Ekkor DFE szög 180-(90-(delta/2)+delta/2)=90
|
 |
| Előzmény: [230] BohnerGéza, 2005-04-28 21:55:56 |
|
| [230] BohnerGéza | 2005-04-28 21:55:56 |
 53. feladat: (egyben segitség az 50,-hez) Az ABC háromszög BC és CA oldalaira, mint alapra, kifelé ( vagy mindkettőt befelé) rakjuk a BDC ill. a CEA egyenlő szárú háromszögeket. A D-nél delta, az E-nél 180 fok mínusz delta szög legyen. Jelöljük AB felezőpontját F-fel. Bizonyítandó, hogy a DEF háromszögben F-nél derékszög, D-nél delta/2 szög van!
(Használjuk fel, hogy a forgatás helyettesíthető két tengelyes tükrözéssel!)
|
|
|
| [228] tudniakarok | 2005-04-20 22:03:19 |
 Nem tudom,hogy volt-e már,de ez egy igen érdekes, tanulságos és egyszerű? feladat:(Napóleon egyik feladata)
52.feladat: Osszunk fel egy r sugarú kört négy egyenlő területrészre! KIZÁRÓLAG KÖRZŐT használhatunk!
|
|
| [227] BohnerGéza | 2005-04-14 22:32:17 |
 Az előző hozzászólás feladata legyen az 50. feladat! Talán némi segítség a megoldásához:
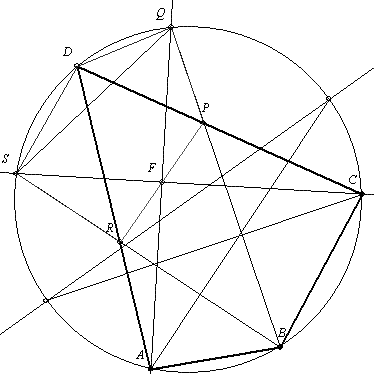
51. feladat: Legyen az 50. feladatban F a PR felezőpontja. Igazoljuk, hogy a QSF háromszögben F-nél derékszög van és Q-nál a B-nél lévő szög fele.
|
| Előzmény: [226] BohnerGéza, 2005-04-12 12:35:53 |
|
| [226] BohnerGéza | 2005-04-12 12:35:53 |
 Az ABCD húrnégyszögben (AB<BC és AD<DC) az A-ból a B belső szögfelezőjére állított merőleges messe BC-t P-ben, a körülírt kört Q-ban, hasonlóan a D belső szögfelezőjére állított merőleges DC-t R-ben, a kört S-ben. Igazolandó, hogy a BS, a DQ és a PR egyenesek egy pontban metszik egymást.
|
|
|
| [224] Hajba Károly | 2005-03-22 09:30:17 |
 Üdv a Geométereknek!
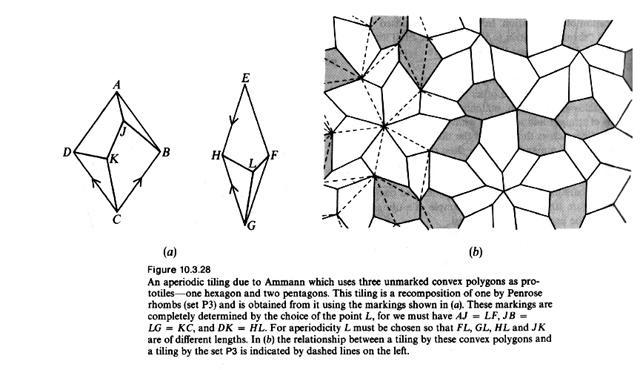
Két érdekes Penrose féle csempe kerestetik. Ha valaki ismeri, szóljon! Közölje itt a paramétereit! :o)
Az alábbi idézet ebből a cikkből való.
"Bármelyik, sárkányokról és dárdákról szóló tétel átalakítható a Penrose-rombuszokról szóló tétellé, vagy akármelyik Penrose-féle csempepárról szólóvá, és viszont. Conway a sárkányokkal és dárdákkal dolgozik szívesebben, más matematikusok jobban szeretik az egyszerűbb rombuszokat. Robert Ammann elképesztően sokféle nem periodikus csempekészletet talált ki. Az egyik készlete, amely két konvex ötszögből és egy konvex hatszögből áll, az élek bármilyen eltorzítása vagy színezése nélkül kényszeríti ki a nem periodikus csempézést. Több olyan hatszögekből álló párt talált, ahol a hatszögek öt belső szöge 90 fokos, egy pedig 270 fokos. E készletek leírása és figyelemre méltó tulajdonságaik tárgyalása megtalálható Branko Grünbaum és G. C. Shephard "Some Problems on Plane Tilings" című könyvében."
Az alábbi kép az idézett könyvből való, de ez nem az 1. keresett csempekészlet.
Ha valaki tud segíteni, azt előre is megköszönöm.
HK
|
 |
|
| [223] Hraskó András | 2005-03-22 06:04:11 |
 Csak úgy a poén kedvéért egy újabb megközelítés a Géza 206. problémájához és a 210-es általánosításhoz.
Tekintsük a k kört a hiperbolikus geometria Cayley Klein modellje alapkörének (lásd Kós Géza írását: itt.)
Ha tekintünk egy A pontot a körön belül, és a kör pontjait átvetítjük A-n át a körre, akkor igazából a hiperbolikus geometriában az A-ra vonatkozó középpontos tükrözés hatását tekintjük a sík végtelen távoli pontjain.
Ha A a körön kívül van, akkor a transzformáció az A polárisának megfelelő hiperbolikus egyenesre vonatkozó tengelyes tükrözés.
Ha A, B, C egy egyenesen vannak (és mind kívül), akkor a három tengelyes tükrözés három egy ponton átmenő egyenesre történik. Ez a pont az ABC egyenes pólusa.
Innen a megoldás a 208. hozzászólásban leírttal analóg.
Persze, ha A, B, C közt van belső pont is, akkor kissé más a helyzet, de ezt meghagyom gondolkoznivalónak.
|
|
| [222] lorantfy | 2005-03-21 10:09:41 |
 Kedves András!
Köszönöm a hozzásolásodat! A térbeli ábra azért született, mert Desargues perspektív háromszögekre vonatkozó tételére gondoltam, ahol a két háromszöget két metsző síkra helyezve, gyakorlatilag nincs mit bizonyítani, hiszen a megfelelő metszéspontok, csak a két sík közös egyenesén lehetnek.(Pirossal és zölddel szineztem a két síkban futó egyeneseket.) Tehát síkban valami elveszik ami térben még nyilvánvaló.
|
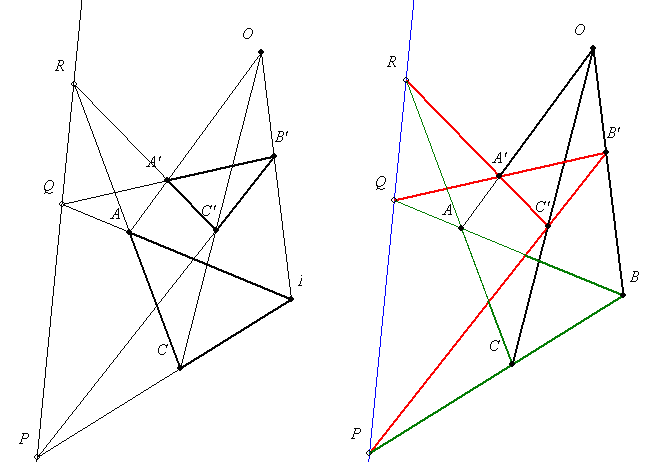 |
| Előzmény: [221] Hraskó András, 2005-03-21 05:25:19 |
|
| [221] Hraskó András | 2005-03-21 05:25:19 |
 Kedves László!
Nem egészen értem, hogy és miért készíted a térbeli ábrádat, de fontos dolgot kapisgálsz az biztos.
Ha jól látom, Pascal tételének volt egy lényeges szerepe a matematika történetében és ez nagyon hasonlatos az itt történt eseményekhez.
Pascal saját tételét egy oldalon hirdetésként tette közzé, bizonyítás nincs is rajta, csak Desargues tevékenységére való utalás van és az a megjegyzés, hogy a kúpszeletet átvetítheti körbe, így elég körre bizonyítani.
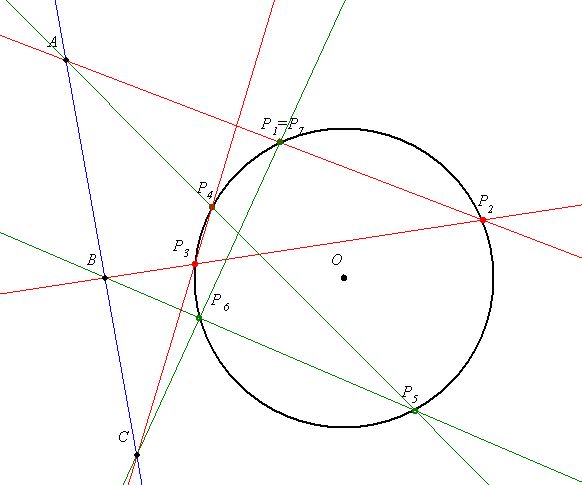
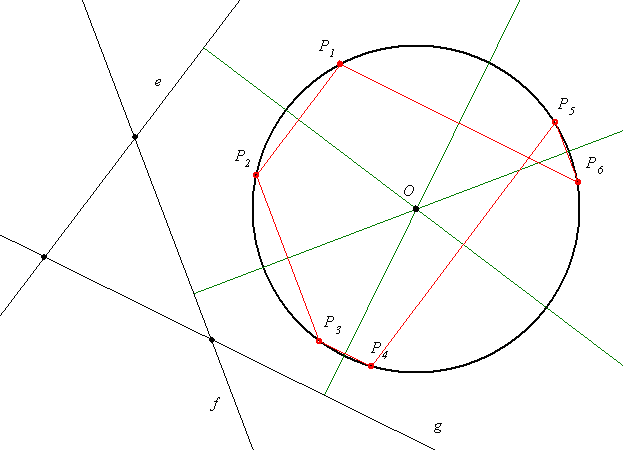
Poncelet a XIX. században újra elővette a problémát. Így kezdi: a Pascal tétel körre egyszerűen igazolható, ha két metszéspont (pld P1P2 P4P5 és P2P3 P4P5 és P2P3 P5P6) az ideális egyenesen van. Ez lényegében Géza eredeti (206. hozzászólás) feladata. P5P6) az ideális egyenesen van. Ez lényegében Géza eredeti (206. hozzászólás) feladata.
Ezután Poncelet arra hivatkozik, hogy bármely kör és egyenes átvetíthető a tér egy pontjából egy másik síkra, úgy, hogy a körből kör legyen, az egyenes pedig az ideális egyenesre képződjék.
Ez szép feladat abban az esetben, ha az eredeti kör és egyenes nem metszi egymást (érdemes elolvani hozzá - és kijavítani - Sain Márton: Nincs királyi út című könyvében az Apollóniuszról szóló részt).
Ellentmonádosnak látszik abban az esetben, ha a kör és az egyenes metszi egymást. Azt hiszem az "egyszerű" bizonyításnak ez a gátja is inspirálhatta Poncelet-t, hogy megalkossa a komplex projektív teret és a körök közös ideális pontjának fogalmát.
|
|
| [220] lorantfy | 2005-03-19 23:07:34 |
 Kedves András!
Gratulálok! Nagyon szép gondolat. Valami hasonlóra gondoltam, csak persze sokkal primitívebb módon:
Az A,B,C pontokra vonatkozó középpontos hasonlóságokat kétszer "oda-vissza" alkalmazva a pontokban állított - ábra szerint keletkező - síkra merőleges szakaszokra végül a P7P7'=P1P1' egyenlőséghez jutnánk, ami már elegendő lenne a bizonyításhoz. Sajnos 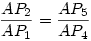 nem teljesül. Az ábra kicsit bonyodalmasnak tűnik, de érdemes megvízsgálni. Két síkról van szó, melyek metszésvonala AC egyenes. nem teljesül. Az ábra kicsit bonyodalmasnak tűnik, de érdemes megvízsgálni. Két síkról van szó, melyek metszésvonala AC egyenes.
|
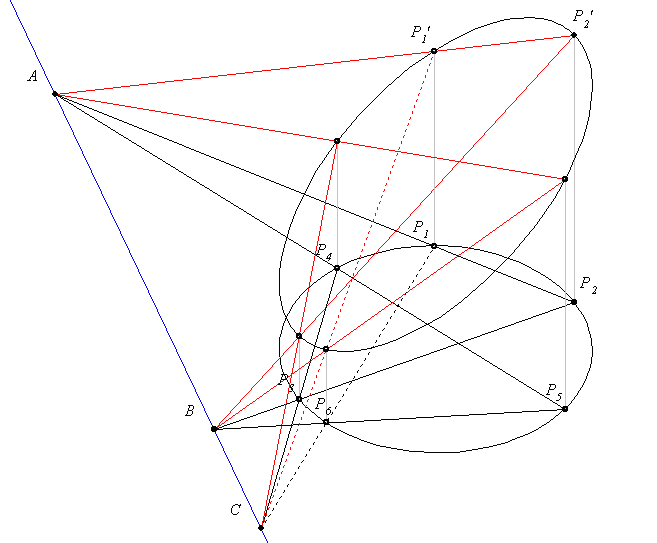 |
| Előzmény: [219] Hraskó András, 2005-03-16 23:29:08 |
|
| [219] Hraskó András | 2005-03-16 23:29:08 |
 Kedves Szefoharcos!
Köszönöm a szép megoldást.
Egy további általánosítás is igaz. A kört (másodrendű görbét) és az A, B, C pontok egyenesét összevonhatjuk egyetlen harmadrendű görbévé.
Az E harmadrendű görbe egy O pontja meghatározza a görbe önmagára való leképezését a következő módon. Ha P E akkor legyen P' az a pont, amelyre O, P és P' valamely egyenesnek a harmadrendű görbével való (multiplicitással számítva) három metszéspontja. Nevezzük ezt a transzformációt az E görbe O centrumú tükrözésének.(Vigyázat O nem feltétlenül fixpontja e leképezésnek, hiszen O képe a görbe O-beli érintőjének E-vel való további metszépontja!) E akkor legyen P' az a pont, amelyre O, P és P' valamely egyenesnek a harmadrendű görbével való (multiplicitással számítva) három metszéspontja. Nevezzük ezt a transzformációt az E görbe O centrumú tükrözésének.(Vigyázat O nem feltétlenül fixpontja e leképezésnek, hiszen O képe a görbe O-beli érintőjének E-vel való további metszépontja!)
Állítás: az E-tükrözések olyanok mint a sík középpontos tükrözései, azaz:
0. E-tükrözés négyzete identikus.
1. Három E-tükrözés kompozíciója is E-tükrözés. (Ebből következik az eredeti tétel, hiszen abban az A, B, C, A, B, C centrumú E-tükrözések kompozíciójáról van szó és az első három kompozíciója megegyezik az utolsó hároméval, így 0. szerint kész is vagyunk.
2. A két E-tükrözés kompozíciójából származó transzformációk olyanok, mint a sík eltolásai, azaz csoportot alkotnak, és az identitáson kívül egyiknek sincs fixpontja.
Géza feladta a labdát, ez véletlenül épp a doktorim témája, lásd
http://matek.fazekas.hu/portal/tanitasianyagok/Hrasko_Andras/doktori/index.html
|
|
| [218] BohnerGéza | 2005-03-16 17:48:13 |
 Szefoharcos megoldása rögtön egy teljesebb általánosítást is elbírt volna, azaz a kör helyett tetszőleges másodrendű görbéből ( egyenespárból is ) kiindulhatunk. Játéknak sem rossz ilyeneket egy szerkesztőprogrammal ( pl, Euklides-szel ) rajzolgatni.
|
| Előzmény: [216] szefoharcos, 2005-03-16 00:54:05 |
|
|
| [216] szefoharcos | 2005-03-16 00:54:05 |
 Sziasztok!
Érdekes megfogalmazása ez a feladat a Pascal-tételnek. Ha ugyanis egy kicsit belegondolunk, látszik, hogy erről van szó. Vegyük azt az álapotot, amikor eljutunk a P6 ponthoz! Ekkor van egy húrhatszögünk; persze a pontokat index szerinti sorrendben kell tekinteni. A megfelelő "szemközti oldalpárok" metszéspontja közül A és B már adott. A Pascal-tétel miatt a harmadik metszéspont rajta van AB egyenesén, és persze P3P4-en, így az csak C lehet. Tehát P6,P1 és C kollineáris; ezt fogalmazta meg a kitűző úgy, hogy CP6 egyenese a kört P1-ben metszi. A Papposz-Pascal-tétel ellipszisre is igaz, ezzel a feladat általánosítása is rögtön adódik.
|
|
|
| [214] lorantfy | 2005-03-14 22:12:22 |
 Hello Attila!
Ezek a feladatok nagyon egyszerűek, de én azért el tudom képzelni, hogy van akinek ezek is problémát okoznak. Az első lépéseket is meg kell tenni és ezek a legnehezebbek, csak vannak akik erre már nem emlékeznek.
A magasságok merőlegesek az oldalakra, így a magasságok talppontjaiban derékszögek vannak. Ha AB felezőpontjából rajzolsz egy kört AFc sugárral, akkor a Thálesz tétel szerint ezen a körön rajta lesz mindkét magasság talppontja. Tehát egyenlő (sugár) távolságra vannak az oldal felezőpontjától.
A háromszög területét ki tudod számítani az oldal és a hozzá tartozó magasság szorzataként. Tehát az oldalak és a magasságok között fordított arányosság van, hiszen szorzatuk állandó. Ekkor viszon az oldalak és a magasságok reciprokai között egyenes arányosság van, mivel ezeket használva a terület képletekben a hányadosok lesznek állandók, ugyanis a magassággal való szorzás helyett oszthatunk a reciprokával.
Ha két szög összege 180 fok, akkor a feleik összege 90 fok.
|
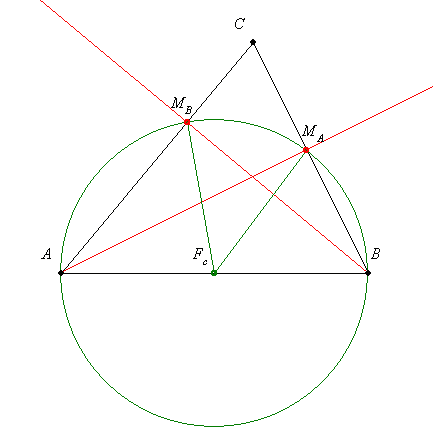 |
| Előzmény: [213] Attila89, 2005-03-14 18:52:48 |
|
| [213] Attila89 | 2005-03-14 18:52:48 |
 Hello mindenkinek!Kaptam 3 feladatot,melyek hát kicsit kifogtak rajtam.Nagyon hálás lennék,ha valaki,még ha csak az egyikben is tudna segíteni.Előre is köszönöm.Az első: Bizonyítsuk be,hogy egy háromszög magasságának talppontjai egyenlő távolságra vannak a harmadik oldal felezőpontjától. A második: Igazoljuk,hogy a háromszög oldalai és a hozzájuk tartotó magasságok reciprokai között egyenes arányosság van. A harmadik: Bizonyítsuk be,hogy a háromszög bármelyik csúcsából induló belső és külső szögfelező merőleges egymásra. És tényleg köszönöm a segítséget.
|
|
|
|
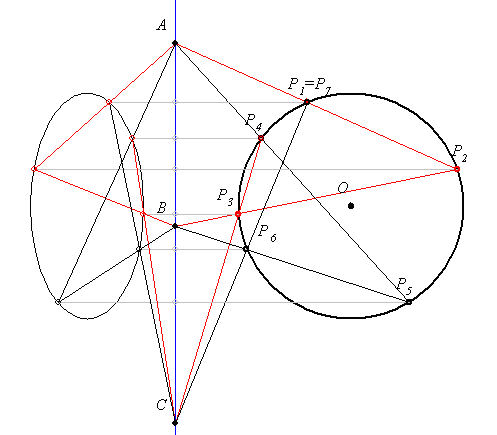
| [210] Hraskó András | 2005-03-01 23:40:11 |
 Általánosítsuk Géza 206-os felszólalásban kitűzött példáját. Az általánosításnak két fokozatát látom, egyelőre csak az elsőt mondom el, hátha rájön valaki a további általánosításra.
Legyen adott a k kör és az A, B, C kollineáris pontok a síkon. Tekintsük a k kör tetszőleges P1 pontját, és k további Pk pontjait úgy, hogy P1P2 átmenjen A-n, P2P3 a B-n, P3P4 a C-n, P4P5 megint A-n, P5P6 a B-n, végül P6P7-t a C-n. Igazoljuk, hogy P7=P1.
|
|
|
| [208] BohnerGéza | 2005-02-28 22:24:20 |
 A [206]-ban szereplő feladat egy megoldása Hraskó Andrástól:
Az adott iránnyal párhuzamos húzás helyett alkalmazzunk tengelyes tükrözést, az irányra merőleges, a kör kp-ján átmenő egyenesre. Csak azt kell igazolni, hogy a t1 t2 t3 t1 t2 t3 kompozíció az identitás, ami nem nehéz.
/ Az első három és a második tükrözés szorzata is ugyanarra az egy tengelyre tükrözéssel helyettesíthető. /
|
| Előzmény: [206] BohnerGéza, 2005-02-21 23:55:14 |
|









 P4P5 és P2P3
P4P5 és P2P3
 E akkor legyen P' az a pont, amelyre O, P és P' valamely egyenesnek a harmadrendű görbével való (multiplicitással számítva) három metszéspontja. Nevezzük ezt a transzformációt az E görbe O centrumú tükrözésének.(Vigyázat O nem feltétlenül fixpontja e leképezésnek, hiszen O képe a görbe O-beli érintőjének E-vel való további metszépontja!)
E akkor legyen P' az a pont, amelyre O, P és P' valamely egyenesnek a harmadrendű görbével való (multiplicitással számítva) három metszéspontja. Nevezzük ezt a transzformációt az E görbe O centrumú tükrözésének.(Vigyázat O nem feltétlenül fixpontja e leképezésnek, hiszen O képe a görbe O-beli érintőjének E-vel való további metszépontja!)