Fórum: Kürschák-verseny

Ennek a feladatnak spec ott van a megoldása a GEOMETRIA topicban..

Sajnos nem jó, mivel az 1003 páratlan. Első gondolatom nekem is ez volt. De ekkor ez nem lehetne ezen a versenyen feladat. Két év múlva egyébként jó lenne a megoldás, aztán négyévente.

Ellenpélda: Legyenek Ai-vel, illetve megfelelően Bi-vel (i=1, 2, 1003) jelölve a két szabályos sokszög csúcsai. ekkor pl. az A1B2- höz (általában) nincs párhuzamos szakasz.

Veszel két db szabályos 1003 szöget, úgy, hogy a két lap egymás eltolt képe, de nincsenek egy síkban. Ez nyilván megadható, és a feladatnak is eleget tesz szerintem. Ha nem jó, ekkor bocs...

De igen :P Bármely két elemének különbsége legalább t. Sorry for that :P

nem úgy volt, hogy "legalább t"? bocs ha rosszul emlékszem :)

Ne haragudj, de a 2. feladatot nem értem. "Bármely két taguk különbsége t" mit akar jelenteni?

Sajnos a feladatok papírját elhagytam, így nem lesz szó szerinti a feladatok szövegezése, de remélem, attól még korrekt marad:

(1) (ahogy a szomszéd GEOMETRIA topicban is olvasható):

Létezik-e olyan 2006 pontból álló halmaz a térben, amelyre igaz, hogy:

a) Nincs minden pontja egy síkban

b) Semelyik három pont sincs egy egyenesen

c) Bármely A és B ponthoz található olyan (tőlük különböző) C és D pont, hogy AB egyenes párhuzamos CD egyenessel.

(2) Legyen a,t,n egész, 1an. Vegyük az {1,2,...,n} halmaz azon részhalmazait, amelyekre igaz, hogy bármely két taguk különbsége t. Bizonyítandó, hogy ezek közül az a-t nem tartalmazóak száma legfeljebb t²-szerese az a-t tartalmazók számának.

(3) Osszunk szét valahogy egy asztalt körbeülő n ember közt n-1 db kártyát. Ezek után egy lépésben egy olyan ember, akinek legalább 2 kártyája van, egy-egy kártyát ad a két szomszédjának. Bizonyítsuk be, hogy bármilyen sorrendben lépnek is, véget ér a folyamat (azaz n-1 embernél 1 kártya, egynél pedig egy se lesz)

Üdv.

Mik voltak az idei feladatok?

Előre is köszi.

No, és az idei kürschák hogy sikerült nektek?

Szerintem ezek a feladatok könnyebbek voltak, mint a tavalyiak, és nem csak én lettem egy évvel okosabb :P (Már csak azért is, mert az Osztályunkban minden feladatra született megoldás, holott tavaly senki nem oldotta meg az elsőt...)

Hello, A dicseretekrol lehet tudni valamit?

Elore is koszi, Racz Miki

Köszönöm a választ!

I. díj nincs, mert senki sem oldotta meg az 1. feladatot.

II. díjat kapott Erdélyi Márton, Gyenizse Gergő, Jankó Zsuzsanna, Paulin Roland, Sümegi Károly és Szilágyi Csaba. Ők megoldották a 2. és a 3. feladatot.

III. díjat kapott Magda Gábor, Nagy Csaba és Seres Gyula. Ők is lényegében megoldották a 2. és a 3. feladatot, de a dolgozataikban voltak kisebb pontatlanságok, amik miatt a megoldásuk nem teljes.

Tudja már vki, mik lettek az idei eredmények?

Bocsánat, az évekkel vagyok zavarban :D

bocsi 16.

lásd 17. hozzászólás

Valaki nem tenné meg, hogy beírja az idei feladatokat?

Sokan megköszönnék...(szierintem, köztük jómagam is)

Üdvözlöm az oldal olvasóit! Milyen nehezek voltak az idei feladatok? Én az utolsó 2 feladattal foglalkoztam.

A 2005. évi Kürschák József Matematikai Tanulóverseny feladatai

1. feladat:

Legyen N>1 és legyenek a₁,a₂,...,a_N olyan nemnegatív valós számok, amelyek összege legfeljebb 500. Bizonyítandó, hogy létezik olyan k1 egész szám és léteznek olyan 1=n₀<n₁<...<n_k=N egészek, amelyekre teljesül, hogy

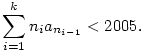
2. feladat:

A és B teniszeznek. Az a játékos győz, aki elsőként nyer meg legalább négy labdamenetet úgy, hogy ellenfelénél legalább kettővel több labdamenetet nyert. Tudjuk, hogy az A játékos minden labdamenetet, a korábbiaktól függetlenül, p1/2 valószínűséggel nyer meg. Bizonyítsuk be, hogy az A játékos győzelmének valószínűsége legfeljebb 2p².

3. feladat:

2×1-es dominókból tornyot építünk a következő módon. Először elrendezünk 55 dominót úgy, hogy egy 10×11-es téglalapot fedjenek le; ez lesz a torony első szintje. Erre azután további, 55 dominót tatalmazó szinteket építünk, ügyelve arra, hogy minden egyes szint pontosan illeszkedjék az előzőre. Az így kapott építményt akkor nevezzük stabilnak, ha a 10×11-es téglalap minden rácsponttól különböző, belső pontja felett van dominónak belső pontja. Hány szintből áll a legalacsonyabb stabil torony?

Köszi, nekem ez kellett. Csak nem értem, h ez miért nincs seholse kiplakátolva az ELTÉn...

Bp-en a BME Informatikai épület IB028 sz. előadótermében (Bp, XI. Magyar Tudósok krt. 2.)

Máshol is van, ha esetleg nem bp-en laksz... :P

És hol? (Ezt is akartam kérdezni, csak kimaradt.)

Október 7 (péntek), 14 órakor.

Pontosan mikor és lesz az idei Kürschák?

Fel is lettek rakva a diák, itt megtalálhatod. A Kürschák 3. feladat általánosítása a diákon a 7. feladatként szerepel. Sajnos néhány dia elég lassan töltődik be, mert az ábrák mind háttérképként vannak, így ha valakinek egy diára kattitntva csak két-három betű jelenne meg, akkor csak várjon türelmesen :-). Sajnos egyes matematikai karakterek nem jelennek meg jól minden böngészőben, de nincs túl sok ilyen (néhány unió stb.).