Angol nyelvű szám, 2002. december
	Előző oldal	Tartalomjegyzék	Következő oldal	MEGRENDELŐLAP

Solutions of problems B

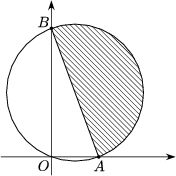
B. 3463. The diameter of a semicircular sponge is 20 cm long. Find the area wiped by the sponge in the corner of the floor of a room if the endpoints of the diameter slide along the two walls enclosing a right angle.

Solution. The sponge is a semicircular disc of diameter AB. If A is moving along the x-axis and B is moving along the y-axis then the circle of diameter AB passes through O. Therefore, no point of the wiped region is farther away from the point O than 20 cm, no points outside the quadrant of radius 20 cm centred at O can be reached by the sponge.

The points of the quadrant of radius 10 cm centred at O are covered by the semicircles whose diameters lie along the x and y axes (Figure 2).

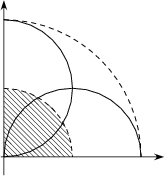Figure 1	Figure 2	Figure 3

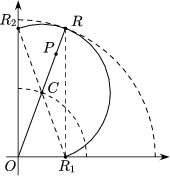
If P is a point of the ``ring'' bounded by the two arcs and OP intersects the larger arc at R, let R₁ and R₂ denote the projections of R onto the axes. Then OR₁RR₂ is a rectangle with diagonals RO=R₁R₂=20 cm. If C is the centre of the rectangle, then OC=10 cm, C lies on the smaller arc, and P lies on the segment CR. The point P is thus contained in the right-angled triangle R₁RR₂, which is entirely contained in the semicircle of diameter R₁R₂ passing through R. Thus the point P is wiped by the sponge.

Therefore, the area wiped by the sponge consists of the points of the closed quadrant of radius 20 cm centred at O, and hence the area wiped is

\(\displaystyle \frac{1}{4}\cdot20^2\pi=100\pi~\rm cm^2. \)