New exercises and problems in Mathematics
September 1997
New exercises for practice in September 1997
C. 473. Can it happen for a whole calendar year that no single Sunday falls on the seventh day of a month?
C. 474. A passanger has been walking for 3.5 hours, covering exactly 5 km in the course of any period of one hour. Is it possible that his average speed during his walk exceeded 5 km/h?
C. 475. In a triangle ABC, a point P on median CC1 is selected such that CP/PC1=m/n. Find the ratios in which P divides the segments of lines AP resp. BP lying inside the triangle.
C. 476. In a right circular cone, both the diameter of the base and the slant height are 20 cm. Find the maximum length of a 2 cm wide self-adhesive band that can be sticked on the lateral surface of the cone without any creasing, cutting, or overlapping.
New exercieses in September 1997
Gy. 3142. Find the smallest positive integer that is divisible by 28, ends in 28 (in decimal system), and the sum of whose digits is 28.
Gy. 3143. Draw a chessboard on the plane. Let A1,
A2, ..., A32 and B1,
B2, ..., B32 denote the midpoints of
the white and the black fields, respectively. Let furthermore P
be any point of the chessboard. Prove that
A1P2+ A2P2+
A32P2= B1P2+
B2P2+ B32P2.
Gy. 3144. Decide if 7/17 can be expressed as 1/a+1/b, where a and b are positive integers.
Gy. 3145. Solve inequality 
Gy. 3146. Let a and b denote the lengths of the
legs of a right triangle, and r its inradius. Prove that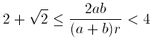 
Gy. 3147. Let P be a point inside a regular hexagon, and e a line incident to P and parallel to a side of the hexagon. Draw five additional lines passing through P such that among the six lines, any two consecutive lines form an angle of 30o. These lines divide the hexagon into 12 regions. Prove that these 12 regions can be divided into three groups such that the sum of the areas of the regions is the same in each group.
Gy. 3148. Let e1, e1 and e1 be three pairwise skew edges of a cube. Select a point Ei on each edge ei for i=1,2,3. Find the locus of the centroids of the triangles E1E2E3.
Gy. 3149. In a triangle ABC, side AB is of unit length. The angles which include this side measure 15o and 60o, respectively. Find the lengths of the two other sides of the triangle without the help of trigonometric functions.
New problems in September 1997
F. 3184. Prove inequality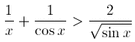 
.
F. 3185. Consider a binary operation defined by 
on the set of numbers not less than 1. Prove that the operation satisfies
the associative law.
F. 3186. The non-negative numbers 
satisfy 
for
. Prove inequality
.
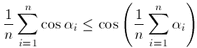F. 3187. Find those triangles which satisfy a2+b2+c2=8R2 where a, b, c and R denote the lengths of the sides and the circumradius of the triangle, respectively.
F. 3188. There are given a circle centered at O, a point A selected on the circle, and a straight line d passing through O. A secant starting at A intersects the circle and line d at points B and D, respectively. Prove that upon rotating the secant about A, in any position, the circle incident to points O, B and D passes through an other fixed point different from O.
F. 3189. Suppose 
are the angles of a triangle. Prove inequality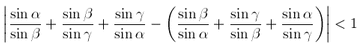 
.
New advanced problems in September 1997
N. 144. Let n denote an arbitrary positive integer. Prove that 2.(3n)! is divisible by n!(n+1)!(n+2)!.
N. 145. Does there exist a polynomial f(x,y,z) of real coefficients such that, f(x,y,z) is positive if and only if |x|, |y| and |z| are the sides of a triangle?
N. 146. Prove that any rational number r in (0,1) of odd
denominator can be expressed in the form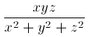 
with suitable integers x, y and z.
N. 147. Is it always true that in a tetrahedron, an inner point of each face can be selected such that they form the vertex set of a regular tetrahedron?