Matematikából kitűzött gyakorlatok és feladatok
1997. szeptember

Általános iskolások részére javasolt példák: C. 473., C. 474., Gy. 3142.

A pontversenyben kitűzött C gyakorlatok

C. 473. Előfordulhat-e egy naptári évben, hogy egyetlen vasárnap sem esik hetedikére?

C. 474. Egy gyalogos 3,5 órát gyalogolt. Bármely 1 órás időszak alatt 5 km utat tett meg. Lehet-e az átlagsebessége nagyobb, mint 5 km/óra?

C. 475. Az ABC háromszög CC₁ súlyvonalán vegyük fel azt a P pontot, amelyre 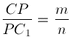( 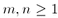tetszőleges egész számok). Milyen arányban osztja P az AP, illetve a BP egyenesnek a háromszögbe eső szakaszát?

C. 476. Egy egyenes kúp alapkörének átmérője és alkotója is 20 cm. Legfeljebb milyen hosszú öntapadó csík ragasztható a kúp palástjára gyűrődés, szakadás (vágás) és átfedés nélkül, ha a csík szélessége 2 cm?

A C gyakorlatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1997. október 15.

A pontversenyben kitűzött gyakorlatok

Gy. 3142. Melyik az a legkisebb 28-cal osztható pozitív egész szám, amelynek a 10-es számrendszerbeli alakja 28-ra végződik, és számjegyeinek összege 28?

Gy. 3143. Rajzoljunk a síkra egy sakktáblát. Legyen a fehér mezők középpontja A₁, A₂, ..., A₃₂, a fekete mezők középpontja B₁, B₂, ..., B₃₂, P pedig a sakktábla egy tetszőleges pontja. Bizonyítsuk be, hogy A₁P²+ A₂P²+ A₃₂P²= B₁P²+ B₂P²+ B₃₂P². (H)

Gy. 3144. Felírható-e a 7/17 szám 1/a+1/b alakban, ahol a és b pozitív egészek?

Sarinay Dávid, Siófok

Gy. 3145. Oldjuk meg az 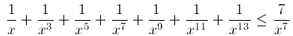egyenlőtlenséget.

Gy. 3146. Egy derékszögű háromszög befogói a és b, beírható körének sugara pedig r. Mutassuk meg, hogy .

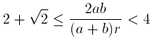Varga István, Békéscsaba

Gy. 3147. Legyen egy szabályos hatszög belső P pontján átmenő e egyenes párhuzamos a hatszög egyik oldalával. Húzzunk P-n át még öt egyenest úgy, hogy az összesen hat egyenes közül bármely két szomszédos 30^o-os szöget zárjon be. Az egyenesek a hatszöget 12 részre osztják. Mutassuk meg, hogy e 12 rész három csoportba osztható úgy, hogy az egyes csoportokban lévő részek területeinek összege megegyezik. (H)

András Szilárd, Kolozsvár

Gy. 3148. Legyen e₁, e₁ és e₁ egy kocka három kitérő éle. Határozzuk meg az E₁E₂E₃ háromszögek súlypontjainak halmazát, ha E_i az e_i él egy pontja (i=1,2,3).

Gy. 3149. Az ABC háromszög AB oldala 1 egység, a rajta levő szögek pedig 15^o és 60^o. Határozzuk meg a háromszög másik két oldalának hosszát trigonometrikus függvények használata nélkül.

Gáspár Merse Előd, Budapest

A pontversenyben kitűzött feladatok

F. 3184. Bizonyítsuk be, hogy 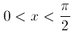esetén .

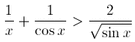F. 3185. Bizonyítsuk be, hogy az 1-nél nem kisebb számokra értelmezett 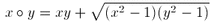művelet asszociatív.

Pataki János, Duino, Olaszország

F. 3186. Tegyük fel, hogy a nemnegatív 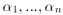számokra 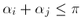teljesül, ha 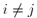. Bizonyítsuk be, hogy .

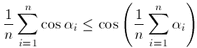Javasolták: Páles Csaba, Debrecen, Pap Gyula, Debrecen és Vörös Zoltán, Budapest

F. 3187. Melyek azok a háromszögek, amelyekre a²+b²+c²=8R², ahol a, b, c a háromszög oldalainak, R a körülírt kör sugarának hosszát jelöli?

Schmidt Edit, Budapest

F. 3188. Adott az O középpontú kör egy A pontja és egy O-n átmenő d egyenes. Egy A-ból induló szelő a kört B-ben, a d-t D-ben metszi. Bizonyítsuk be, hogy ha a szelő A körül forog, bármely helyzete esetén az O, B, D pontokon átmenő kör O-n kívül átmegy még egy fix ponton.

F. 3189. Egy háromszög szögei 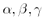. Bizonyítsuk be, hogy .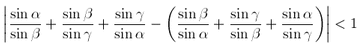

Mihalovics Sándor, Esztergom

A pontversenyben kitűzött nehezebb feladatok

N. 144. Legyen n tetszőleges pozitív egész. Mutassuk meg, hogy 2^.(3n)! osztható n!(n+1)!(n+2)!-sal.

N. 145. Van-e olyan f(x,y,z) valós együtthatós polinom, amely pontosan akkor pozitív, ha az |x|, |y|, |z| hosszúságú szakaszokból háromszög szerkeszthető?

Benkő Dávid, Budapest

N. 146. Igazoljuk, hogy a (0, 1) intervallumba eső tetszőleges páratlan nevezőjű r racionális számhoz találhatók olyan x, y, z egészek, hogy az 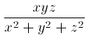r-rel egyenlő.

N. 147. Igaz-e, hogy tetszőleges tetraéder lapjain van egy-egy olyan belső pont, hogy azok egy szabályos tetraéder csúcsai?

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1997. október 15.