New exercises and problems in Mathematics
October 1997

New exercises for practice in October 1997

C. 477. A game machine accepts two kinds of coins: red and green ones. For each coin the machine returns 5 coins of the other kind. One starts playing with 1 green coin. Can it happen that after a while he has as many green coins as red ones?

C. 478. In an arithmetic progression, the sum of the first n terms and the sum of the first 2n terms are A and B, respectively. Express the sum of the first 3n elements in terms of A and B.

C. 479. The lengths of the bases of a trapezium are a and c, respectively. Find the length of the segment parallel to the bases which halves the area of the trapezium.

C. 480. In a tetrahedron, two of the faces are equilateral triangles of unit side. The two other faces are right isosceles triangles. Find the volume of the tetrahedron.

New exercises in October 1997

Gy. 3150. In a certain town, each bus line has 3 stops. Any two bus-stops are connected with a line, and any two lines have a common bus-stop. How many bus lines may be there in the town?

Gy. 3151. For any positive integer n, let A_n denote the set of positive integers which are not relatively prime to n. Find all integers n for which 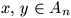implies .

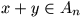Gy. 3152. The real numbers a, b, c, d satisfy 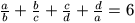and . Find all possible values of .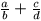

Gy. 3153. Find the minimum value of expression 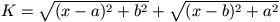, where a and b are positive parameters.

Gy. 3154. The sides of a triangle ABC are denoted by a, b, c, according to the standard notation. The lengths of the tangents from vertices A, B, C to the incircle are x, y and z, respectively. Assuming , prove inequality .

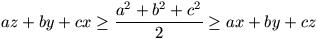Gy. 3155. Prove that in any triangle, a line passing through the incenter halves the perimeter of the triangle if and only if it halves the area of the triangle.

Gy. 3156. In a triangle, the segments of the medians lying inside the inscribed circle are all of the same length. Does this imply that the triangle is equilateral?

Gy. 3157. In a tetrahedron, the segments of the medians lying inside the inscribed sphere are all of the same length. Does this imply that the tetrahedron is regular?

New problems in October 1997

F. 3190. Is there any real number x>1 which is not an integer and still satisfies inequality ?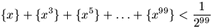

F. 3191. The positive integers n and p satisfy 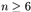and 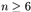. Colour p vertices of a regular n-gon with red, colouring the remaining vertices with blue. Prove that there exist two congruent polygons of at least 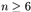vertices such that each vertex of the first polygon is red and each vertex of the second one is blue.

F. 3192. Is it possible to move a knight on a 5x5 chessboard so that it returns to its original position after having visited each field of the board exactly once?

F. 3193. May a non-planar quadrilateral have only right angles?

F. 3194. In a right triangle ABC, construct the point D on the hypotenuse AB such that triangles DCA and DCB have equal inradii.

F. 3195. The whole surface of a cube shaped cake (including its bottom) is covered with chocolate. The cake is to be distributed among K people so that each of them receives the same amount of cake, and also the same amount of chocolate cover at the same time. In order to accomplish this task, we divide the cake into NxNxN alike cube shaped pieces, and give everybody the same number of pieces, taking care that the total surface area of the chocolate covered sides of the pieces one gets is also the same for everybody. Is it possible to realize this for an arbitrary K? At least how many pieces are necessary for K=1997?

New advanced problems in October 1997

N. 148. There are given 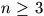pairwise distinct points in the plane. Prove that there are three distinct points A, B and C among them which satisfy inequality .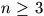

N. 149. The sequence (a_n) is defined by the recursion a₀=a₁=1, (n+1)a_n+1=(2n+1)a_n+3na_n-1. Prove that the sequence consists of integer numbers.

N. 150. There are given in the plane a parabola and points P and Q outside the parabola such that line PQ passes through the focus of the parabola. Draw two tangents to the parabola from each of points P and Q. Prove that the four points of intersection obtained this way lie on the same circle.

N. 151. The sequence a₂, a₃, ... consists of positive real numbers such that 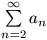converges. Prove that series 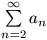is also convergent.