New exercises and problems in Mathematics
December 1997

New exercises for practice in December 1997

C. 485. We are given a 100x100 array of numbers such that, for k=1,2,...,100, its kth row is an arithmetic progression whose first term is 1, and whose common difference is k. Find the largest entry along the diagonal that connects the lower left corner of the array to its upper right corner.

C. 486. How many different ways can some 1, 2, 5, 10 and 20 forint coins make 25 forints?

C. 487. Given that 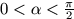, prove inequality .

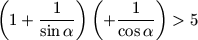C. 488. The lateral surface of a frustum of a right circular cone is coloured with two colours; it is blue below the middle of its slant height and is red above that. Find the ratio between the radii of the bases of the frustum, given that the surface area of the blue part is twice as large as that of the red part.

New exercieses in December 1997

Gy. 3166. Compare the following two numbers: 1997¹⁹⁹⁹ 1999¹⁹⁹⁷

Gy. 3167. Prove that two positive integers a and b have the same parity if and only if there exist positive integers c and d such that a²+b²+c²+1=d².

Gy. 3168. In a set of size 15, find 15 subsets, each of size 7, such that any two of them have exactly 3 elements in common.

Gy. 3169. Find all triangles with integer side-lengths in which one of the angles is twice as large as an other one.

Gy. 3170. A triangle ABC has a right angle at vertex C. The bisector of the angle at B intersects side AC and the circumcircle at points P and Q, respectively. Find the measures of the angles of the triangle, given that BP=2PQ.

Gy. 3171. The lengths of the sides of a certain triangle are integers, one of them being 1. Is it possible that the inradius of the triangle is a rational number?

Gy. 3172. A right circular cylinder shaped vessel, whose axis is vertical, is filled up with water. The radius of the cylinder is 10 cm, its height is 25 cm. Find the amount of water which flows out of the vessel when it is tilted by 30^o. Construct the angle by which the vessel should be tilted from its original position if we want to pour out half of the water it contains.

Gy. 3173. Given three straight lines in the space, each incident to a given point P, construct a plane through P which forms the same angle with each of the given lines.

New problems in December 1997

F. 3202. Let 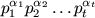be a positive integer written in canonical form. Let r₁, r₂, ..., r_m denote those positive integers which are smaller than n and are relatively prime to n. Derive equality .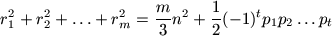

F. 3203. Prove that any set of size 15 contains 15 subsets, each of size 6, such that any two of them have either 1 or 3 common elements.

F. 3204. There is given a heap of 923^k pebbles. Two players play the following game. They move alternately, removing at each turn either 9, 2 or 3 pebbles from the heap. The one who cannot move, loses the game. Which player has a winning strategy?

F. 3205. In an arbitrary triangle, let a, b, c denote the lengths of the sides of the triangle, and let m_a, m_b, m_c, respectively, denote the lengths of the corresponding altitudes. Prove inequality .

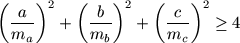F. 3206. We are given a circle k₁, and points H₁, H₂ and P outside the circle. Construct a circle k₂ passing through P such that, for i=1,2, the lengths of the tangents from H_i to k₂ are the same as the lengths of the tangents from H_i to k₁.

F. 3207. A regular tetrahedron, whose edges are 2 units long, is inscribed into a right circular cylinder in such a way that it has two vertices on the perimeter of each base of the cylinder. Find the volume of the cylinder.

New advanced problems in December 1997

N. 155. In an infinite sequence of positive integers, each term has the same number of divisors. Prove that there is an infinite subsequence in which any two terms have the same greatest common divisor.

N. 156. Suppose that a₁,a₂,... and b₁,b₂,... are integer sequences such that a₁=b₁=0, and a_n=nb_n+a₁b_n-1+a₂b_n-2+a₃b_n-3+...+a_n-1b₁ holds for . Prove that, for any prime number p, a_p is divisible by p.

N. 157. An nxn array consists of real numbers such that the entries are monotone decreasing in each row and each column of the array. Whenever we are given a number a, our task is to decide if the array contains that number or not. For that purpose, we may compare a with any entry in the array. How many comparisons do we have to make to solve the problem for sure, regardless of the specific value of a?

N. 158. There are given 9 convex subsets of (3-dimensional) space such that any 8 of them have a lattice point in common. Prove that there exists a lattice point which is contained in each set.