Matematikából kitűzött gyakorlatok és feladatok
1998. január

Általános iskolások részére javasolt példák: C. 489., C. 490., Gy. 3179.

A pontversenyben kitűzött C gyakorlatok

C. 489. Jóska és Karcsi kirándulásuk során az erdőből egy olyan műútra érnek, amelyen autóbusz közlekedik. Elhatározzák, hogy buszra szállnak. Jóska a következő megállóhoz igyekszik, Karcsi viszont vissza az előző megállóhoz, mivel az szerinte közelebb van. A buszt mindketten éppen elérik. Igaza volt-e Karcsinak, ha ő 6 km/h, Jóska 4 km/h, az autóbusz 60 km/h sebességgel haladt az úton?

C. 490. Bizonyítsuk be, hogy két páratlan négyzetszám különbsége osztható 8-cal.

C. 491. Bizonyítsuk be, hogy bármely háromszögben legfeljebb egy olyan oldal van, amely a hozzá tartozó magasságnál kisebb.

C. 492. Megmértük egy vízszintes terepen álló torony emelkedési szögeit a torony talppontjától 50 m-re és 100 m-re. A mért szögek összege 45^o. Milyen magas a torony?

A C gyakorlatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1998. február 15.

A pontversenyben kitűzött gyakorlatok

Gy. 3174. Aladár és Bea a következő játékot játsszák: Rajzolnak egy nxn-es négyzetet, vízszintes oldalait piros, a függőlegeseket kék ceruzával. Aladár egy lépés során pirosra fest egy kis négyzetet, ha az még nincs kiszínezve, és legalább egy oldala piros. Bea ugyanezt teszi kékkel. Aladár össze szeretné kötni az alsó és felső oldalt piros mezők élben szomszédos sorozatával. Bea ugyanígy szeretné összekötni a függőleges oldalakat. Az nyer, aki (előbb) el tudja érni a célját. Felváltva lépnek, Aladár kezd. Ha valaki már nem tud lépni, a játék döntetlen. Milyen n-ek esetén van valamelyikőjüknek nyerő stratégiája? (H)

Javasolta: Pap Gyula, Debrecen

Gy. 3175. Tetszőleges pozitív számokra igazoljuk a következő egyenlőtlenséget: .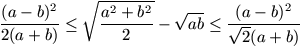

Javasolta: Czirok Levente, Szekszárd

Gy. 3176. Az (a_i) sorozatot a következőképpen definiáljuk: a₁=0, a₂=2, a₃=3, 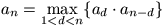(n=4,5,6,...). Határozzuk meg a₁₉₉₈ értékét.

Javasolta: Fried Ervin, Budapest

Gy. 3177. A Bajnokcsapatok Európa Kupa legjobb $16$ csapata közé bejutott két magyar csapat is: a Bolyai TC, és az Eötvös TK. Mi a valószínűsége, hogy egymás ellen játszanak? (A verseny egyenes kiesési rendben folyik; két csapat találkozóján az egyik továbbjut, a másik végleg kiesik.)

Javasolta: Pataki János, Duino

Gy. 3178.Legalább milyen hosszú egy egységnyi területű háromszög második legnagyobb oldala?

Gy. 3179. Egy tetraéder csúcsait rendre kék, piros, sárga és zöld színűre festettük. A csúcsokat a színnek megfelelő nagy kezdőbetűkkel jelöltük. Ezután kiszíneztük a tetraéder éleit is úgy, hogy azok színe megegyezzen valamelyik végpont színével, és eközben mind a négy színt újra fölhasználtuk. Bizonyítsuk be, hogy van olyan csúcs, amelyből kiinduló élek közül az egyik kék, a másik piros, a harmadik zöld, vagy a másik három pont közötti élek közül az egyik kék, a másik piros, a harmadik zöld.

Gy. 3180. Egy a, b, c oldalú háromszög területe (a-b+c)(a+b-c). Bizonyítsuk be, hogy a háromszög a oldallal szemközti szöge szögfelezőjének hossza .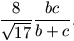

Gy. 3181.Egy szabályos négyoldalú gúla köré írt gömb középpontja egybeesik a beírt gömb középpontjával. Mekkora két szomszédos oldalél szöge?

A pontversenyben kitűzött feladatok

F. 3208. Tegyük fel, hogy az x, y, z pozitív számokra x²+xy+y²=9, y²+yz+z²=16, z²+zx+x²=25. Határozzuk meg xy+yz+zx értékét.

Javasolta: Horváth Gábor, Debrecen

F. 3209. Egy n csúcsú összefüggő gráf minden élére egy valós számot írtunk, ezt nevezzük az él értékének. A gráf bármely útjának súlya legyen a benne előforduló legnagyobb értékű él értéke. A gráf bármely x, y csúcsára jelölje f(x,y) az x-ből y-ba vezető legkisebb súlyú út súlyát. Bizonyítsuk be, hogy az f függvény legfeljebb n-1 különböző értéket vesz föl.

F. 3210. Lehet-e egy kétváltozós valós együtthatós polinom értékkészlete a nyílt 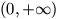intervallum?

F. 3211. Mutassuk meg, hogy ha n>2 egész szám, és 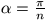, akkor .

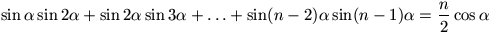F. 3212. Az ABC háromszög BC oldalának felezőpontja F, az A-hoz tartozó belső szögfelező és BC metszéspontja E, az AFE háromszög köré írt körének és az AB, valamint az AC oldalaknak A-tól különböző metszéspontja pedig B₁ és C₁. Mutassuk meg, hogy BB₁=CC₁.

F. 3213. Egy kocka két kitérő élegyenesén mozog egy-egy egységnyi hosszúságú szakasz. A szakaszok melyik helyzetében lesz a végpontjaik által meghatározott tetraéder térfogata maximális?

A pontversenyben kitűzött nehezebb feladatok

N. 159. Bizonyítsuk be, hogy tetszőleges konvex n-szöget háromszögekre lehet bontani n-3 egymást nem metsző átlójával úgy, hogy a sokszögnek egy csúcsa se szerepeljen valamelyik háromszög körülírt körének belsejében.

N. 160. Definiáljuk az (a_n) sorozatot a következőképpen: a₀=a₁=0, a₂=1, a_n+3=a_n+1+1998a_n. Mutassuk meg, hogy tetszőleges pozitív egész n-re .

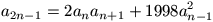N. 161. Legyenek a p polinom együtthatói legfeljebb 1998 abszolút értékű egész számok, és p(2000) prímszám. Igazoljuk, hogy p nem bontható fel két, legalább elsőfokú egész együtthatós polinom szorzatára.

Javasolta: Pap Gyula, Debrecen, Braun Gábor, Budapest

N. 162. A G n-pontú teljes gráfot teljes páros gráfok uniójára szeretnénk felbontani úgy, hogy G mindegyik éle pontosan egy páros gráfban szerepeljen. Hány teljes gráfra van ehhez szükség?

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1998. február 15.