Exercises and problems in Physics
March 1998
New experimental problem:
m. 196. Pour some sand into a transparent, cylindrical container, and fill it up with water. Close the bottle, shake it well, and stand it in a vertical position. Observe how the sand settles in the bottom. Find a relation between the volume of sediment (settled sand) and time. Find a method to determine the size of the sand particles.
New exercises:
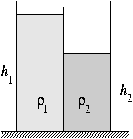
FGy. 3140. An open rectangular tank is divided into two
equal halves by a vertical wall. In the left half of the tank is a column of
liquid, density
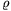1=800 kg/m3,
and height h1=30 cm. The right half of the tank contains
liquid of density
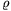2=1600 kg/m3,
to a height h2=20 cm (see figure). The two liquids don't mix.
- a) Find the heights of the respective columns, if a small hole is drilled
in the bottom of the separating wall.
- b) Where is it possible to drill a hole, without causing any change to
the state of the system?
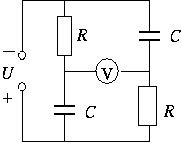
FGy. 3141. Consider the circuit shown in the figure
(R=1 k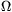
,
C=25 nF, U=25 V).
What is the p.d. shown on the ideal (static) voltmeter?
FGy. 3142. Coal is mined in the Equatorial-Guinea, to be burnt in power stations across the world. How does this change the angular velocity of the rotation of the Earth?
FGy. 3143. A piston operated vacuum pump is connected to a gas discharge tube of ten times its volume. How many times does the piston need to be pumped in order for the pressure in the discharge tube to decrease to 1/10th of its original value? Assume the process to be
- a) isothermal;
- b) adiabatic (
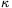=1.4).FGy. 3144. A binary star is at a distance of 100 parsec from the Earth. The absolute brightnesses of its components are 2m and 4m respectively. What is the absolute brightness of the whole system?
New problems:
FF. 3145. Distilled water is poured on top of a colloidal solution in a container. The two liquids don't mix. The angle of incidence of a laser beam entering the water from air is 5o greater than its angle of refraction, and the angle of incidence from the water at its interface with the solution is 6o greater than its angle of refraction. Find the velocity of the beam in the colloidal solution, if the refractive index for light travelling from air to water is 1.333.
FF. 3146. An aeroplane, with a wing span of 50 m, travels at a
speed of 900 km/h. The vertical component of the Earth's magnetic field is
0.5 mT. Find the p.d. induced between the wing tips. Why doesn't a bulb,
designed for this voltage, light up if it is connected between the wing
tips? Is it possible to measure the p.d.?
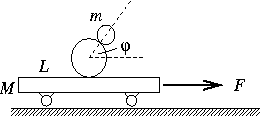
FF. 3147. In a demonstration, two balls of equal density, and
radii, r and R=2r, are placed on the middle of a cart
of mass M=6 kg and length L=2 m. The mass of smaller ball is
m=1 kg. The balls are caused to roll, without slipping, in such a way
that the larger ball is at the bottom, and a strait line connecting their
centres remains constant at an angle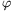 
to the horizontal. The cart is pulled with a horizontal force in the
direction shown in the figure.
- a) Find the magnitude of the force, F.
- b) How much time elapses before the balls fall down?
FF. 3148. The primary coil of a transformer has N1
turns, and self-inductance, L. The secondary coil has
N2 turns, and is connected to a load resistor, R.
(The ohmic resistance of the coils is negligible.) An alternating emf of
frequency, f, is applied across the primary coil. Determine the phase
difference between the primary and secondary voltages and currents. Examine
the limiting cases,
R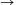
0 and
R
.
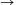
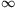Under what conditions are the currents in the coils inversely proportional to
the number of turns?
New advanced problem:
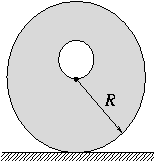
FN. 3149. A hole of radius R/4 is drilled through a solid, homogeneous cylinder, lying on a rough, horizontal surface, as shown in the figure. With what period does the cylinder move to and fro, if it is displaced slightly from its equilibrium position?