Exercises and problems in Physics
May 1998
New experimental problem:
m. 198. Determine the number of carbon atoms per millimetre on lines drawn with pencils containing graphite leads of various hardness.
New exercises:
FGy. 3160. The height of a brick is 15 cm, its density is 2.5 g/cm3. What is the maximum possible height of a wall built out of such bricks of the pressure at the base is not to exceed 0.5 MPa? The thickness of the mortar layer between the bricks is 1.5 cm and its density of 1.5 g/cm3.
FGy. 3161. The temperature of some plants rises considerably when they are in blossom. A plant of that kind is put in a thermally insulated vessel with a heat capacity of 18 J/K. Initially, the temperature of the air enclosed is 20 oC, and it rises to 25 oC in 40 seconds. Then, after a quick airing, it only takes 30 seconds to raise the temperature from 20 oC to 25 oC again. Find the heat generating power of the plant.
FGy. 3162. A series combination of three voltmeters is connected across the poles of a battery with relatively large internal resistance and an electromotive force of 9 V. One voltmeter reads 2.4 V, the other reads 2.9 V and the third one reads 3.6 V. What will the same voltmeters read if they are connected to the battery in parallel?
FGy. 3163. A pendulum swings in front of a scale between the divisions marked 10 and 30. In photograph of the pendulum, the blurred image covers the region between the marks of 18 and 25. Find the time of exposition if the period of the pendulum is 1.73 seconds.
FGy. 3164. The initial speed of the centre of a ping pong ball spinning ``backwards'' on a level tabletop is 3 \rm m/s, and the tangential speed of its rotation os 9 m/s initially. The coefficient of friction is 0.2.
- a) Find the time it takes the ball to get back to its starting
position.
- b) For that speeds will the ball come to rest on the table instead of coming back?
New problems:
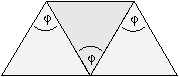FF. 3165. A direct-vision prism is made out of three prisms,
each with a refracting angle of
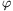=60o, attached to each
other as shown in the figure. Light of a certain wavelength is incident on the
first prism. The angle of incidence is 30o and the ray leaves the
third prism parallel to the direction of incidence. The refractive index of
the glass of the first and third prisms is 1.44. Find the refractive index of
the material of the middle prism.
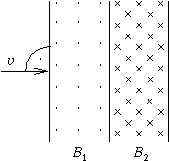FF. 3166. The magnetic field shown in the figure consists of
two uniform regions. The width of the first part is 5 cm, and the
magnetic induction here is 0.001 T. The width of the other part is also
5 cm, with the direction of the induction being opposite in direction and
0.002 T in magnitude. What should be the minimum speed of the electron
arriving from the direction indicated in the figure so that it can pass
through the magnetic field? How much time does such an electron spend in the
magnetic field?
FF. 3167. Find the average power drawn out of an object oscillating at a frequency f with an amplitude A by a taut string attached to it, in which the speed of elastic waves is c and its mass per unit length is \mu.
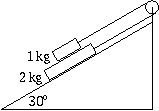FF. 3168. A 2-kg block is placed in an inclined plane enclosing a
30o angle with the horizontal, and a 1-kg block is placed on top
of it. The two of them are connected by a thread wrapped over a pulley as
shown in the figure. The coefficient of friction between the blocks in 0.1 and
0.2 between the lower block and the slope. Find the acceleration of each block
and the tension in the thread.
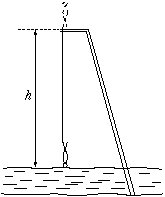
FF. 3169. A person of height h0=2 m is doing bungy jumping from a tower of h=25 m over the lake Balaton. One end of an elastic rope is attached to his foot and the other end is fixed in the tower. He starts falling from rest in vertical position. The length and elastic properties of the rope are chosen so that the speed of the descending person should decrease to zero at the instant when his head reaches the surface of the water. At the end the person is hanging from the rope with his head 8 m over the water.
- a) Find the unstretched length of the rope.
- b) Find the maximum speed and the maximum acceleration during the
jump.
New advanced problem:
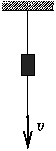
FN. 3170. Consider the following well-known experiment: There is an object suspended from a thread and having an identical string attached to the bottom. If the lower string is pulled slowly, the upper one will break. If it is jerked abruptly, it is the lower string that will break. Let the mass of the object be m=0.2 kg. Let the force constant of the strings be D=1000 N/m and let the maximum tension they can withstand be Fmax=6mg. Which string will break if the lower end is pulled with a speed of
- a) 0.15 m/s,
- b) 0.28 m/s,
- c) 0.40 m/s,
- d) 0.80 m/s.