 |
Exercises and problems in Physics |
New experimental problem:
m. 200. The remote control handset of the TV set emits invisible infra-red radiation. Examine to what extent different sheets of paper let this radiation through or reflect it.
New exercises:
FGy. 3184. A sports field covered with snow is cleared using a snow-plough that travels at a uniform speed and pushes the snow in front of it to the opposite side of the field. The field is twice as long as it is wide. How should the machine move in the field to minimise the work done: crossways or lengthways? What is the ratio of these works?
FGy. 3185. A student connects four identical cells of 1.5 V
each and an accumulator of 6 V in series. He connects a resistor of
6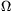 
to this `battery', the pd across
this resistor is also 6 V. He then takes away 1, 2, 3 and then 4 cells
from the circuit and is surprised to see that the pd across the resistor
remains 6 V in each case. After some reasoning, he realises that there
is nothing surprising in this. Why?
FGy. 3186. A monatomic ideal gas expands at a constant pressure, while its energy increases by 3 kJ. How much work does it do? How much heat does it take up?
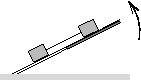FGy. 3187. Two bodies with a mass of 2 kg each are at rest on a
horizontal board. The bodies are joined by a tight thread of negligible
mass. One end of the board is slowly lifted. The coefficient of friction is
0.2 for the body at the bottom and 0.5 for the one at the top. What
force stretches the thread when the bodies already slide?
FGy. 3188. The little prince arrives at a planet with a small back-pack. He can calculate the density of the planet using the following three observations:
- a) On the Earth, he could jump four times as high
without his back-pack than with it.
- b) On this planet, he can jump K
times as high with his back-pack than the distance covered by the planet in
the meantime.
- c) Sending his back-pack on orbit around the planet, he can
catch it in time t. What is the density of the planet?
FGy. 3189. A student made pictures of the comet Hale-Bopp with an exposition time of 4 minutes. Due to the rotation of the Earth, the stars made `streaks' in the pictures. Estimate the angular velocity of the rotation of the Earth using the following data: the focal length of the objective of the camera is 300 mm, the enlargement of the negatives is 4-fold and he measures the trace of a star to be 23 mm.
New problems:
FF. 3190. Where should a rod of homogeneous mass distribution be hung so that the period of this pendulum is the minimum possible?
FF. 3191. A thin metal rod is rotated at a constant angular velocity
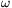about an axis crossing the middle of
the rod and perpendicular to the rod, in a magnetic field parallel to the axis
of rotation. What is the charge distribution inside the rod?
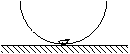
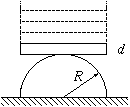FF. 3192. Place a domino on top of a half-cylinder lying on its flat
face as shown in the figure. When the domino is deviated by a small
angle and then released, it starts a periodic oscillation on top of the
half-cylinder. How many dominoes can be placed on top of each other to allow
such oscillations? What can the maximum deviation be so that the dominoes do
just not slip from the half-cylinder if the static coefficient of friction
between them is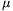 
=0.1?
(The thickness of a domino is d=5 mm, the
radius of the cylinder is R=3 cm.)
FF. 3193. A beetle of mass M climbs from the bottom of a thin
hemispherical shell of radius R and mass M to its top rim.
- a) What work does it do?
- b) What is the minimum static coefficient of friction
between the beetle and the hemispherical shell if the beetle can climb?
- c) Does the friction between the horizontal table and the hemispherical
shell play any role?
New advanced problem:
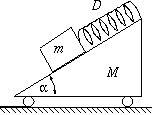FN. 3194. What is the frequency of the oscillation of the body of
mass M shown in the figure if all frictions are negligible?