New exercises and problems in Mathematics
October 1998
 |
New exercises for practice in October 1998 |
C. 513. A 25 meter long wound cable is cut into 2 and 3 meter long pieces. How many different ways can this be done if also the order of pieces of different lengths is taken into account?
C. 514. Let Sn denote the sum of integers contained in the open interval (2n, 2n+1). Prove that Sn is divisible by 3 for every positive integer n. Determine those values of n for which Sn is divisible by 9.
C. 515. A cube is divided into 27 pairwise congruent smaller cubes. Find the maximum number of small cubes that can be stabbed by a straight line.
C. 516. Prove that any tetrahedron has an altitude which is at least twice as large as the diameter of the sphere inscribed in the tetrahedron.
 |
New exercieses in October 1998 |
Gy. 3222. Let A and B denote 9-digit numbers. Assume that, upon replacing any digit of A by the corresponding digit of B (that is, the digit of B of the same place value), we obtain a number divisible by 7. Prove that this is also true in the other way around, that is, upon replacing any digit of B by the corresponding digit of A, we get a multiple of 7.
Gy. 3223. Let x, y, z denote positive real numbers. Prove or disprove the following statements.
- a) If
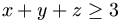 ,
then
,
then 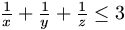 .
.- b) If
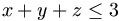 ,
then
,
then 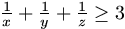 .
.English competition problem
Gy. 3224. Determine all solutions in positive integers K, M, n of the system of equations
n+k=(n,k)2
k+m=(k,m)2
m+m=(m,n)2,
Gy. 3225. A sequence (ai) is defined by
a1=1 and a1=1, 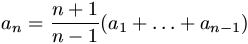 .
Determine a1998.
.
Determine a1998.
Gy. 3226. Two circles k1 and k2 intersect each other at points A and B. The line tangent to k1 at A intersects k2 at a point C, the line tangent to k2 at B intersects k1 at a point D. Prove that BD2.BC=AC2.AD.
Gy. 3227. Two figures are inscribed in a circle. One is a trapezium based on a diameter of the circle, the other is an isosceles triangle whose legs are parallel to the legs of the trapezium, respectively. Prove that the two polygons have equal areas.
Gy. 3228. A cyclic quadrilateral has sides of length 2, 3, 4 and 6, in this order. Determine the two ratios in which the diagonals divide each other.
Bodó Boglárka (Budapest)
Gy. 3229. Prove that the space can be tiled by congruent copies of regular tetrahedra and congruent copies of regular octahedra of the same length of edge.
 |
New problems in October 1998 |
F. 3244. Find all positive numbers x that are solutions to some equation of the form 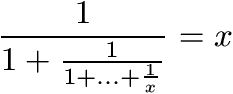 .
.
F. 3245. A squirrel hoarded hazel-nuts for the winter. On the first day of the winter he ate 1 nut and 1 percent of the remaining ones. On the second day he ate 2 nuts plus 1 percent of the rest, and so on, until the nth, last day of the winter, when he ate the last n nuts that remained. How many nuts did the squirrel gathered for the winter?
F. 3246. Let x1 denote a positive number less than 1,
and consider the sequence defined recursively by the rule
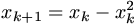 . Prove that
. Prove that
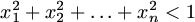 , no matter how large n is.
, no matter how large n is.
F. 3247. Given a quadrilateral ABCD, point K (L) is obtained as the intersection of ray AB (AD) with the circle centered at A whose radius is the geometric mean of the sides of the quadrilateral starting at vertex A. Similarly, points M and N are obtained as the intersections of rays CB and CD, respectively, with the circle centered at C whose radius is the geometric mean of the sides starting at vertex C. Find the right condition which guarantees that KL=MN.
F. 3248. There are 5 girls and 5 boys at a party. Participants who belong to the same sex do not know each other. Moreover, there cannot be found two girls who know the same two boys. At most how many acquaintances can be among the participants of the party? How will the answer change if there are 7 girls and 7 boys at the party?
F. 3249. In a convex polyhedron, every face has an odd number of sides and every vertex has an odd valence (that is an odd number of attached edges). Is it possible that the number of triangle faces and the number of vertices of valence 3 sum up to 9?
 |
New advanced problems in October 1998 |
N. 183. The parabola y=x2 is rolled, without slipping, along the x-axis. How far away can the parabola move from the y-axis?
N. 184. An infinite tree graph is given in the plane such that every lattice point is a vertex of the graph, and every edge of the graph connects two lattice points whose (Euclidean) distance is at most 1998. Prove that there exist two points in the plane, a unit distance apart, such that the path which connects them in the tree is at least 101998 long.
N. 185. Find a polynomial of several integer variables with integer
coefficients whose range consists of certain negative numbers and the numbers
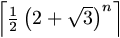 (n=1,2,...).
(n=1,2,...).
N. 186. For a certain real number x and a positive integer n, both cos nx and cos (n+1)x are rational numbers. Does it follow that cos x, too, is a rational number?
