Exercises and problems in Physics November 1998

New experimental problem:

m. 201. Measure the speed dependence of pace-length and of the rate of paces, ranging from a slow stroll to fast running.

New exercises:

FGy. 3195. When sacking, a basketball player rises vertically to 76 centimetres. How much time does he spend then in the lower and upper 15 centimetres of his trajectory? Why do we get the feeling that players are soaring in the air?

FGy. 3196. 100 MJ of electrical energy per second needs to be transmitted to consumers through a 20-kilometre aluminium cable of 100 mm² cross-section. What is the loss, if the p.d. is 100 kV at the point of consumption? What would the loss be at 380 V?

FGy. 3197. A homogeneous rod of 1.5 m length and 3.36 cm diameter is hanging, fixed at one end. A 2-kilogram ball collides elastically at a horizontal velocity of 0.3 m/s with the lower end of the rod. Meanwhile, it has transmitted its full kinetic energy to the rod bouncing away. What material do you think the rod may have been made of? At what angular velocity did the rod start moving? How much later did it pass the initial position again?

FGy. 3198. At the bottom of a glass there is a liquid the density of which is three times as much as that of water. Above this liquid there is water. The two materials do not mix. There is also a piece of ice in the glass, with a piece of aluminium frozen into it. How do the levels of liquids change when the ice melts?

New problems:

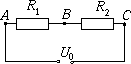FF. 3199. In the electric circuit shown in the figure R₁=400 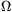, R₂=600 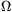, U₀=50 V. The internal resistance of the battery is negligible. If a voltmeter is attached between points A and B, it measures 19.5 V. What is the resistance of the voltmeter? What p.d. does it feature between points B and C? How many times do we need to increase the resistance of the voltmeter in order to decrease the relative errors of the voltage measurements below 1 %?

FF. 3200. Two blocks connected with a spring are moving on a horizontal surface. The coefficient of kinetic and static friction is 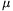. How does the system's centre of mass move? Data: D=10 N/m, m₁=m₂=0.4 kg, v_1,0=0, v_2,0=2 m/s, 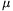=0.3.

FF. 3201. A small block of mass m and electric charge Q is sliding without friction from the top of a cylinder whose radius is R and the axis is horizontal. The cylinder is placed into a homogeneous magnetic field, B is parallel to the axis of the cylinder. Where does the small block leave the surface of the cylinder? Is it possible that it does not leave it at all?

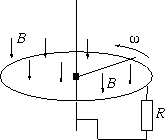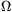FF. 3202. A horizontal 50-cm metallic rod is attached to a vertical conductive axis and it can rotate around it. The other end of the metallic rod touches a conductive ring. Between the ring and the axis there is a 0.1  resistor. The resistance of all other conductors and the friction are negligible. The equipment is placed into a vertical homogeneous magnetic field of 0.8 T magnetic induction. What torque is to be exerted on the rod in order that it should rotate at a constant 10 s^-1 angular velocity?

New advanced problem:

FN. 3203. In a thermally insulated, easily expandable gas-bag there is some gas. The pressure of the environment decreases from p₁ to p₂ Therefore, the gas expands and cools down. In which case does the temperature go down more: when the outer pressure decreases slowly or drops dramatically?