New exercises and problems in Mathematics
December 1998
 |
New exercises for practice in December 1998 |
C. 521. An amount of 1512 forints is made up of HUF 2, 5, 10, 20, 50, 100 and 200 denominations (containing at least one of each). There are 1512 different ways to distribute this money between our left and right pockets, including the two cases when one of our pockets is empty. (We do not make any distinction between pieces of the same denomination.) How many pieces does the sum contain of each denomination?
Proposer: Bakonyi Gábor, Budapest
C. 522. Find all lines, tangent to the parabola defined by equation y=x2, which form an angle of 45o with the segment that connects the focus of the parabola to the point of tangency.
C. 523. A spherical cap is cut off a ball of radius R such that the curved surface area of the cap is c times larger (c>1) than the area of the circular cross-section. Determine the height of the spherical cap.
C. 524. In a triangle ABC, AC=BC. There is given a point P on side AB such that 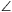 ACP=30o. In addition, point Q outside the triangle satisfies
ACP=30o. In addition, point Q outside the triangle satisfies
CPQ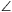 =CPA
=CPA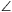 +APQ
+APQ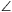 =78o.
=78o.
Given that all angles of triangles ABC and QPB, measured in degrees, are integers, determine the angles of these two triangles.
Proposer: Müncz Márton, Budapest
 |
New exercieses in December 1998 |
Gy. 3238. How many dice must be rolled at the same time to maximize the probability that exactly one 6 occurs among the scores?
Gy. 3239. Determine those integers x, y, z for which
(x -y-1)3+(y -z-2)3+(z -x+3)3=18.
Proposer: Kovács Béla, Szatmárnémeti
Gy. 3240. Each field of a 9x9 ``chessboard'' contains a +1 or -1. First, we simultaneously replace each number with the product of the numbers written in the fields that share an edge with the field containing the given number. We may repeat this step again and again. Is it true that, after a finite number of repetitions, we get back to the original arrangement?
Chinese contest problem
Gy. 3241. Is there any order of the numbers 1, 1, 2, 2, ...,
1998, 1998 in which there are exactly n numbers placed between the two
copies of n, for every 1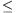 n
n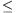 1998?
1998?
Gy. 3242. Connect a point inside a convex quadrilateral to each vertex of the quadrangle. Assuming that the four triangles obtained this way have the same area, prove that the point is incident to one of the diagonals of the quadrangle.
Gy. 3243. Divide the plane into 1000 parts, using the smallest possible number of straight lines.
Gy. 3244. Given two similar triangles of the same orientation, consider the midpoints of the segments that connect the corresponding vertices of the triangles, respectively. Assuming that these points form a triangle, prove that this triangle is similar to the original ones.
Gy. 3245. Find the smallest natural number k for which the following statement is true. If, in a tetrahedron, there are k pairs of edges each forming an angle of 60o, then the tetrahedron is necessarily regular.
 |
New problems in December 1998 |
F. 3256. The sum of the positive real numbers x1, x2, ..., xn is 1. Prove that
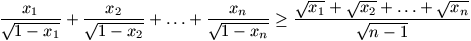
F. 3257. Consider the graph of the function defined by
x 2x3-2x on the interval [-1, 1]. Which two
points of the graph lie at the greatest distance apart?
2x3-2x on the interval [-1, 1]. Which two
points of the graph lie at the greatest distance apart?
F. 3258. The first term of a sequence (an) is a positive integer. The subsequent terms of the squence are defined recursively by the rule
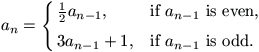
Prove that the sequence must contain a number which is divisible by 4.
F. 3259. In a right-angled triangle, acute angles 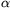 and
and 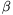 satisfy
satisfy
tan
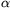 +tan
+tan
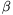 +tan
2
+tan
2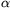 +tan
2
+tan
2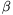 +tan
3
+tan
3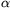 +tan
3
+tan
3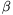 =70.
=70.
Determine the angles of the triangle.
Proposer: Fitos László, Esztergom
F. 3260. Points A1, A2, ..., An, B and C of the plane satisfy
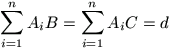 .
.
Moreover,
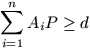
holds for every point P of the plane. Prove that the points A1, A2, ..., An all lie on the same line.
F. 3261. Let v1, v2, v3, v4 be non-coplanar vectors in the 3-space whose sum is 0. Show that there exists a tetrahedron with faces S1, S2, S3, S4 such that for each 1\leq i\leq 4, Si is perpendicular to vi and the area of Si is equal to the length of vi.
 |
New advanced problems in December 1998 |
N. 191. Let Ln denote the nth term of the Lucas squence, defined by L0=2, L1=1, Ln+1=Ln+Ln-1. Let, in addition, a1, a2, ... be a sequence of integers such that
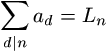
holds for every positive integer n. Prove that n|an for every positive integer n.
N. 192. In a set H, whose elements are certain subsets of the set of all positive integers, any two distinct elements have a finite intersection. Is H necessarily enumerable?
Proposer: Szabó Jácint, Győr
N. 193. Prove that, for any sufficiently large integer
n, there exists a polynomial p of degree at most 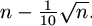 such that
such that
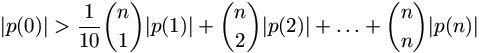 .
.
N. 194. Is it possible to find finitely many positive integers, a1<a2<...<an, with the following two properties:
- all sums of different summands that can be formed of them, including the monomials as well, are different;
- any integer an+1>an, for which all sums, which can be formed from the numbers a1, a2, ..., an, an+1, are different, satisfies an+1>1998an?
Proposer: Kun Gábor, Budapest
