New exercises and problems in Mathematics
January 1999

New exercises for practice in January 1999

C. 525. The Martians' calendar counts 687 days a year. From time immemorial, the months last either 26 or 29 days. The Habitual Innovators suggest to switch over to months that last either 27 or 31 days. They have their plan accepted with the help of the Trimmers who hope that the number of months (and thus the wages, too) can be reduced this way. Is the Trimmers' conception feasible?

C. 526. How many 7-digit numbers exist which are divisible by 9 and whose last but one digit is 5?

C. 527. The two parallel shores of a trapezium-shaped lake are 200 m and 100 m long. The other two shores, respectively, meet these at angles of 90^o and 45^o. Two guards are walking around the lake in the same direction and at the same pace so that they keep the same distance in both directions along the lake. Determine the maximum distance between the two sentries, measured in a straight line across the lake.

C. 528. Three pairwise orthogonal concurrent lines are given in 3-space. Is it possible to place any acute triangle in such a way that its 3 vertices are incident to the 3 lines, respectively?

New exercieses in January 1999

Gy. 3246. A disc is placed on each field of an nxn ``chessboard''. Each disc has a red and a blue face. Two players play the following game. They move alternately. The one who moves picks out a blue disc, and turns every disc over in the rectangle whose upper left corner is the selected disc, lower right corner is the lower right corner of the whole board. The player who cannot move, loses the game. Determine those initial positions when the first player has a winning strategy.

Gy. 3247. Which one of the two numbers 1997^19981999 and 1999^19981997 is greater?

Gy. 3248. Let p denote an arbitrary prime number. Find all nonnegative integer solutions of the equation

.

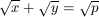Gy. 3249. There are given 2n+1 odd positive numbers, none of which is greater than 6n. Prove that one of these numbers divides an other one. (H)

Gy. 3250. Regular pentagons are arranged to form a ``flower''. Ten segments, each connecting vertices of these pentagons, are drawn, according to the Figure. Prove that they produce a regular 10-gon.

Gy. 3251. In a triangle, the angles opposite to sides a, b, c measure 55^o, 15^o and 110^o, respectively. Prove that c²-a²=ab.

Gy. 3252. Consider those points in 3-space whose three coordinates are all nonnegative integers, not greater than n. Determine the number of straight lines that pass through n of these points.

Gy. 3253. The cross-section of a pencil is a regular hexagon. The sides of the pencil are alternately coloured blue and white. Is it true that, if we look at the pencil ``from afar'', then we see ``the same amount'' of the blue and the white surfaces? 

Javasolta: E. Csóka, Debrecen

New problems in January 1999

F. 3262. Prove that the number 2²¹⁹⁹⁹-1 has at least 1999 different prime factors.

F. 3263. Find the maximum number of 3-term arithmetic progressions one can select from a sequence a₁<a₂<...<a_n of real numbers.

American competition problem

F. 3264. Prove that every positive x satisfies

.

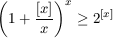F. 3265. In a triangle ABC, let F denote the midpoint of side BC. Prove that

cot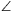FAC-cot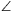FAB=2cot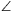AFB.

Javasolta: Z. Vörös, Budapest

F. 3266. Segments AB and CD of the same length are given. Fix AB, and move CD in the plane in such a way that the diagonals AC and BD of the quadrilateral ABCD are both equal to a constant length, too. Find the locus of the intersection point of the diagonals of quadrilateral ABCD.

F. 3267. It is known that, given 3 cottages and 3 wells on the surface of a ball-shaped planet, it is impossible to connect each cottage to each well with a road such that the 9 road segments do not cross each other. Is a similar statement true if the cottages and wells are on a doughnut-shaped planet?

New advanced problems in January 1999

N. 195. A disc is placed on each field of an nxn ``chessboard''. Each disc has a red and a blue face. Two players play the following game. They move alternately. The one who moves, may choose among the following 4 options:

• to turn a blue disc over;
• to turn a blue disc over, and at the same time to turn over all discs lying in the same row to the right of the selected disc;
• to turn a blue disc over, and at the same time to turn over all discs lying in the same column below the selected disc;
• to pick a blue disc out and turn every disc over in the rectangle whose upper left corner is the selected disc, lower right corner is the lower right corner of the whole board.

Based on a problem submitted by T. Kósa, Budapest

N. 196. Lattice points A, B, C, D, E are given in 3-space such that ABCD is a parallelogram. Assuming that pyramid ABCDE has a volume greater than 1/3, prove that it contains (either in its interior or on its boundary) a lattice point other than its vertices.

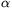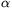N. 197. Let be a real number between 1 and 2, and define a_n=[ⁿ] (n=0, 1, 2, ...). Is it true that all but a finite number of positive integers are expressible as the sum of the elements of some finite subsequence of (a_n)?

N. 198. Two complete graphs, each of n vertices, are given such that a natural number is written at each vertex. Write along each edge the sum of the numbers written at its two endpoints. Suppose that n is not a power of 2. Prove that, if the same numbers, with the same multiplicity, appear along the edges in the two graphs, then a similar statement is true for the vertices of the two graphs, too. 

Submitted by T. Kiss, Budapest