New exercises and problems in Mathematics
February 1999

New exercises for practice in February 1999

C. 529. Find the smallest odd positive integer that has the same number of divisors as the (even) number 360.

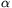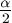C. 530. Prove that the sine and cosine of an angle are both rational numbers if and only if tan is either a rational number or not defined.

Proposer: Z. Hans

C. 531. In the Cartesian system, consider all proper triangles whose vertices have integer coordinates of absolute value at most 1. Find a complete list of the distances of the centroids of these triangles from the origin.

C. 532. Two circles of respective radii r₁ and r₂ touch each other externally. Consider one of their common external tangents. Rotate the segment of this line, which lies between the points of tangency, about the axis that connects the centres of the circles. Express, in terms of r₁ and r₂, the area of the curved surface obtained this way.

New exercieses in February 1999

Gy. 3254. Is there an integer whose cube has a decimal representation of the form ababab1?

Spanish competition problem

Gy. 3255. All the numbers have fallen down one by one from the face of an old wall-clock. Prove that if we replace the numbers, in any order, on the empty face of the clock, there will be three consecutive numbers among them that add up to 20 at least. Is it always true that there will also be a sum greater than 20?

Gy. 3256. Find all (not necessarily positive) prime numbers p, q, r which satisfy

.

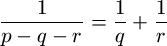Proposer: Á. Kovács, Budapest

Gy. 3257. We have 2 identical mugs. In a 31-storey building, we have to determine the highest floor from which, when a mug is dropped, it still does not break. The experiment we are allowed to do is to drop a mug from a floor of our choice. How many experiments are necessary to solve the problem in any case, for sure?

Proposer: B. Marx, Budapest

Gy. 3258. Find the maximum possible area any hexagon may have whose vertices are the midpoints of the sides of some convex hexagon of unit area.

Gy. 3259. In a circle with centre O, radius OA intersects chord BC perpendicularly at a point M. Let X be an arbitrary point on the longer arc BC, and denote by Y the intersection point of XA and BC, and by Z the point of intersection of the circle with line XM, other than X. Prove that AY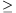MZ.

Gy. 3260. In a rectangular coordinate system a square is drawn with sides forming angles of 45^o with the axes. Is it possible that there are exactly 7 lattice points inside the square?

Gy. 3261. A convex quadrilateral ABCD is given in the plane. Prove that the circles with respective diameters AC and BD, each orthogonal to the plane, intersect each other if and only if the quadrilateral ABCD is cyclic.

New problems in February 1999

F. 3268. Let p denote a prime number of the form 4k+3. Suppose that x, y are positive integers such th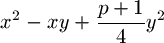at is divisible by p. Prove that there exist integers u,v such that

.

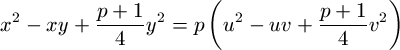F. 3269. Determine the remainder when the number 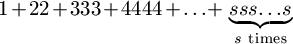, written in base s+1, is divided by s-1.

F. 3270. Consider those polynomials p(x)=x⁴+ax³+bx²+cx+1 whose coefficients are all positive numbers less than 3, and which do not have any real root. Find the maximum value of the product abc.

F. 3271. Given a convex n-gon P₁P₂...P_n, points Q₁, Q₂, ..., Q_n-2 are placed inside the polygon such a way that each triangle P_iP_jP_k contains exactly one of them in its interior. Partition the n-gon into regions by drawing all of its diagonals. Prove that each point Q_l lies in a triangular region of the partition.

Based on an idea of F. Sarlós

F. 3272. In 3-space there are given four pairwise unequal spheres, each lying outside all the others. Each pair of these spheres admits an internal and an external centre of similarity. Consider the straight lines determined by these points. Find the maximum possible number of different straight lines in such an arrangement.

F. 3273. A circle k and a line e containing one of its diameters are given in the plane. An other circle touches e such that the distance between its point closest to k and circle k itself equals to the length of its radius. Find the locus of the centres of all such circles.

New advanced problems in February 1999

N. 199. We have k identical mugs. In an n-storey building, we have to determine the highest floor from which, when a mug is dropped, it still does not break. The experiment we are allowed to do is to drop a mug from a floor of our choice. How many experiments are necessary to solve the problem in any case, for sure?

N. 200. Prove that, for infinitely many positive integers n, there exists a polynomial p of degree n with real coefficients such that p(1), p(2), ..., p(n+2) are different whole powers of 2.

N. 201. Four points u₁, u₂, v₁ and v₂ are given on the complex plane. Consider those two circles, each orthogonal to the plane, whose diagonals are segments u₁u₂ and v₁v₂, respectively. Prove that these circles intersect each other perpendicularly if and only if

.

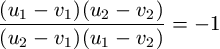N. 202. Let p denote a prime number of the form 4k+3 and let x be any positive integer. Prove that the integer 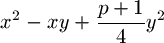does not have any divisor of the form kp-1.