Matematikából kitűzött gyakorlatok és feladatok
1999. február

Általános iskolásoknak javasolt feladatok: C.529, Gy.3254, Gy.3255, Gy.3257, Gy.3258.

A pontversenyben kitűzött C gyakorlatok

C. 529. Melyik az a legkisebb pozitív páratlan szám, amelynek ugyanannyi osztója van, mint a 360-nak?

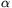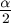C. 530. Bizonyítsuk be, hogy egy szög szinusza és koszinusza akkor és csak akkor racionális egyszerre, ha tg  racionális (vagy nem értelmezett).

Javasolta: Hans Zoltán

C. 531. Tekintsük azokat a valódi háromszögeket, amelyek csúcspontjainak koordinátái egy síkbeli derékszögű koordináta-rendszerben a -1, 0, 1 számok közül valók. Milyen távolságra lehet e háromszögek súlypontja az origótól?

C. 532. Az r₁ és r₂ sugarú körök kívülről érintik egymást. Egyik közös külső érintőjüknek az érintési pontok közé eső szakaszát megforgatjuk a körök centrálisa körül. Fejezzük ki a keletkező csonkakúp palástjának területét r₁-gyel és r₂-vel.

A C gyakorlatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1999. március 16.

A pontversenyben kitűzött gyakorlatok

Gy. 3254. Van-e olyan köbszám, amelynek tizes számrendszerbeli alakja ababab1 alakú?

Spanyol versenyfeladat

Gy. 3255. Öreg falióránk számlapjáról leesett az összes szám. Bizonyítsuk be, hogy bárhogyan összekeverve tesszük is vissza a tizenkét számot, lesz közöttük három egymás melletti, amelyek összege legalább 20. Igaz-e, hogy mindig van 20-nál nagyobb összeg is?

A kolozsvári Matematikai Lapok nyomán

Gy. 3256. Adjuk meg az összes olyan p, q, r (nem feltétlenül pozitív) prímszámot, amelyre

.

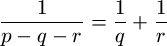Javasolta: Kovács Ádám, Budapest

Gy. 3257. Van két egyforma bögrénk. Meg szeretnénk tudni, hogy egy 31 szintes ház hányadik emeletéről lehet egy ilyen bögrét leejteni úgy, hogy még ne törjön össze. Ehhez a két bögrét a ház különböző emeleteiről kiejthetjük.

Hány kísérletre van szükség a kérdés eldöntéséhez? (H)

Javasolta: Marx Balázs, Budapest

Gy. 3258. Mekkora lehet egy egységnyi területű konvex hatszög oldalfelező pontjai által meghatározott hatszög területe?

Gy. 3259. Az O középpontú kör OA sugarát a BC húr merőlegesen metszi az M pontban. Legyen X a nagyobbik BC ív tetszőleges pontja, XA és BC metszéspontja Y, az XM egyenes és a kör második metszéspontja pedig Z. Bizonyítsuk be, hogy AY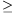MZ.

Gy. 3260. Egy derékszögű koordinátarendszerben megrajzolt négyzet oldalai 45^o-os szöget zárnak be a tengelyekkel. Lehetséges-e, hogy a négyzet belsejében pontosan 7 rácspont található?

Gy. 3261. Adott az ABCD konvex négyszög a síkban. Bizonyítsuk be, hogy a síkra merőlegesen állított AC és BD átmérőjű körök akkor és csak akkor metszik egymást, ha ABCD húrnégyszög. (H)

A pontversenyben kitűzött feladatok

F. 3268. Legyen p egy 4k+3 alakú prímszám. Igazoljuk, hogy ha az x, y pozitív egész számokra 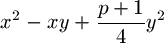osztható p-vel, akkor léteznek olyan u, v egészek, amelyekre

.

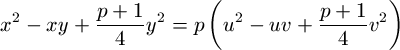F. 3269. Határozzuk meg az s+1 alapú számrendszerben felírt 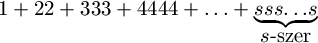összeg (s-1)-gyel való osztási maradékát.

F. 3270. Tekintsük azokat a p(x)=x⁴+ax³+bx²+cx+1 polinomokat, amelyek együtthatói 3-nál kisebb pozitív számok, és amelyeknek nincs valós gyöke. Legfeljebb mekkora lehet abc értéke?

F. 3271. A P₁P₂...P_n konvex n-szög belsejében úgy helyeztük el a Q₁, Q₂, ..., Q_n-2 pontokat, hogy bármelyik P_iP_jP_k háromszög belsejébe pontosan egy esik közülük. Igazoljuk, hogy ha az n-szöget az összes átlója behúzásával felosztjuk, akkor mindegyik Q_l pont egy háromszög alakú tartományba esik.

Sarlós Ferenc ötletéből

F. 3272. Legfeljebb hány egyenest határoznak meg négy, páronként különböző sugarú, egymáson kívül elhelyezkedő gömb páronkénti külső és belső hasonlósági pontjai?

F. 3273. Adott a k kör és annak egy e átmérő egyenese. Határozzuk meg azon körök középpontjainak halmazát, amelyek e-t érintik, k-hoz legközelebbi pontjuknak k-tól való távolsága pedig megegyezik a sugarukkal.

A pontversenyben kitűzött nehezebb feladatok

N. 199. Van k darab egyforma bögrénk. Meg szeretnénk tudni, hogy egy n szintes ház hányadik emeletéről lehet egy ilyen bögrét leejteni úgy, hogy még ne törjön össze. Ehhez a bögréket a ház különböző emeleteiről kiejthetjük. Hány kísérletre van szükség a kérdés eldöntéséhez?

N. 200. Bizonyítsuk be, hogy végtelen sok pozitív egész n-hez létezik olyan n-edfokú valós együtthatós p polinom, amelyre p(1), p(2), ..., p(n+2) különböző 2-hatványok.

N. 201. Adott a komplex számsíkon négy pont: u₁, u₂, v₁ és v₂. A síkra merőlegesen vesszük azt a két kört, amelynek átmérője az u₁, u₂, illetve v₁, v₂ pontokat összekötő szakasz. Mutassuk meg, hogy ez a két kör pontosan akkor metszi egymást merőlegesen, ha

.

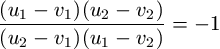N. 202. Legyen p egy 4k+3 alakú prímszám. Igazoljuk, hogy az 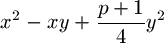számnak semmilyen pozitív egész x-re sincs kp-1 alakú osztója.

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1999. március 16.