Matematikából kitűzött gyakorlatok és feladatok
1999. március

Általános iskolásoknak javasolt feladatok: C. 534, Gy. 3262, Gy. 3263, Gy. 3265, Gy. 3266.

A pontversenyben kitűzött C gyakorlatok

C. 533. Hogyan változik két szakasz szorzata, ha az egységet kétszeresére növeljük?

C. 534. Az első 539 pozitív egész szám közül kiválasztunk néhányat úgy, hogy azok összege legalább egyharmada az eredeti számok összegének. Legalább hány számot kell ehhez kiválasztanunk?

C. 535. Hány olyan pozitív, egymáshoz relatív prím számokból álló (rendezetlen) számpár van, amelyben a számok összege 285?

C. 536. Egy R sugarú gömböt és egy R sugarú, 2R magasságú henger palástját egyforma vastagságú festékréteggel vonunk be. Melyikhez kell több festék?

A C gyakorlatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1999. április 15.

A pontversenyben kitűzött gyakorlatok

Gy. 3262. Mutassuk meg, hogy bármely 3x3-as bűvös négyzet első sorában szereplő számok négyzetének összege egyenlő a harmadik sor számainak négyzetösszegével. (Bűvös négyzetnek nevezzük az olyan nxn-es számtáblázatot, amelynek minden sorában, oszlopában és a két átlójában a számok összege ugyanannyi.)

Javasolta: Kiss Sándor, Nyíregyháza

Gy. 3263. Tekintsük az 1222 és 1999 közötti egész számokat. Válasszunk ki közülük minden lehetséges módon két különbözőt és szorozzunk össze. Mennyi lesz a szorzatok összege?

Gy. 3264. Milyen k természetes számokra igaz, hogy 2^2k+3+3^k+2.7^k osztható 17-tel?

Gy. 3265. Van egy kétkarú mérlegünk és 12 egyforma nagyságú, különböző színű golyónk. Közülük egy más fajsúlyú anyagból készült, mint a többi. Megtudhatjuk-e három méréssel, hogy melyik ez a golyó? El tudjuk-e dönteni még azt is, hogy nehezebb, vagy könnyebb a többinél? (H)

Gy. 3266. Egy húrtrapéz szárainak hossza a, másik két oldala b és c, a két átlója d hosszúságú. Azt állítom, hogy d²-a²=bc. Igaz-e az állításom?

Gy. 3267. A k₁ és k₂ körök a P és Q pontokban metszik egymást. Az A a k₁, a B pedig a k₂ kör egy-egy pontja úgy, hogy az AB szakasz a belsejében tartalmazza Q-t. Legyen AB felezőpontja F. A PF egyenes két új metszéspontja a körökkel C, illetve D. Bizonyítsuk be, hogy F a CD szakaszt is felezi.

Gy. 3268. Ha az y=sin x és az y=sin²x függvények grafikonjait közös koordináta-rendszerben ábrázoljuk, a kapott görbék nemcsak hasonlóak, hanem hasonló helyzetűek is. Mekkora a hasonlóság aránya, és hol lehet a nagyítás középpontja?

Gy. 3269. N város mindegyikéből egy-egy kém indul a hozzá legközelebbi egyik városba. Legfeljebb mekkora lehet N, ha csak két városba érkezik kém? (H)

A pontversenyben kitűzött feladatok

F. 3274. Oldjuk meg az alábbi egyenletrendszert:

x+y+z=0
x³+y³+z³=0
x¹⁹⁹⁹-y¹⁹⁹⁹+z¹⁹⁹⁹=2²⁰⁰⁰.

Javasolta: Nagy Tamás, Zalaegerszeg

F. 3275. Keressük meg a 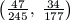nyílt intervallumban a legkisebb nevezőjű törtet.

F. 3276. Jelöljük az ABC rácsháromszög területét T-vel. Bizonyítsuk be, hogy ha

(AB+BC)²<8^.T+1,

akkor A, B és C egy négyzet három csúcsa.

W. L. Putnam Emlékverseny, 1998

F. 3277. Egy szabályos ötszög csúcsaiba a középpontból a v₁, v₂, ..., v₅ vektorok mutatnak. Tegyük fel, hogy a k₁, k₂, k₃, k₄, k₅ egészekre teljesül, hogy k₁v₁+k₂v₂+...+k₅v₅=0. Bizonyítsuk be, hogy ekkor k₁=k₂=...=k₅.

F. 3278. Az y=x³ egyenletű görbe pontjain egy * műveletet értelmezünk a következőképpen. Ha A és B a görbe két pontja, akkor legyen A*B az AB egyenes és a görbe harmadik metszéspontjának az origóra való tükörképe. (Ha a definícióban szereplő valamelyik két pont egybeesik, akkor összekötő egyenesük helyett vegyük a görbe adott pontbeli érintőjét). Mutassuk meg, hogy a * művelet asszociatív.

F. 3279. Adott két, egymással 36^o-os szöget bezáró egyenes. Egy szöcske ugrál ide-oda egyik egyenesről a másikra úgy, hogy minden ugrásának a hossza ugyanakkora. Mutassuk meg, hogy legfeljebb tíz különböző pontba juthat el.

A pontversenyben kitűzött nehezebb feladatok

N. 203. Adott a síkon az ABCD négyszög. A BCD és ACD körök az AC és BC egyeneseket az E, illetve F pontokban metszik. Igazoljuk, hogy

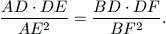
N. 204. Egy szabályos dobókockát n-szer feldobunk. Milyen n esetén lesz pontosan 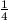annak a valószínűsége, hogy a dobott számok összege osztható 4-gyel?

N. 205. Melyek azok a pontok egy szabályos háromszög belsejében, amelyeken át legalább három, a háromszög területét felező egyenes húzható?

N. 206. Határozzuk meg azokat az f:R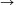R folytonos függvényeket, amelyekre tetszőleges x, y valós számok esetén

f(xy)=f(x)f(y)+f(-x)f(-y)    és    f(x+y)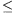f(x)+f(y)

teljesül, továbbá f(1999)=1000.

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1999. április 15.