New exercises and problems in Mathematics
May 1999

New exercises for practice in May 1999

C. 541. Four figures are to be inserted into a six-page essay, in a given order. One page may contain at most two figures. How many different ways are there to assign page numbers to the figures under these restrictions?

C. 542. Find those positive integers n for which the inequality

(n-2)(2+2²+...+2ⁿ)<n^.2ⁿ

holds.

C. 543. Construct a triangle, given one of its angles and two of its altitudes.

C. 544. The `frame' of a unit cube consists of two parallel faces and the edges that connect the two faces. We fix one of the faces and twist the other one about the axis that connects the midpoints of the faces through an acute angle 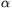, while the length of the connecting edges remains the same. How does this deformation reduce the distance between the parallel faces?

New exercieses in May 1999

Gy. 3278. In a 3x3 magic square, 3 entries a, b and c are given according to the following diagram. Fill the rest of the diagram (so that the sum of the entries in each row, column, and diagonal are the same).

Proposer: S. Kiss, Nyíregyháza

Gy. 3279. Ten children play `undo-the-knot' the following way. First, they form a circle, and with their eyes closed, arms extended, they start moving towards the centre of the circle. Next, with each hand they grab someone else's hand. Finally, they open their eyes and start undoing the knot: they bend down and slip under and step over each other's arm, and so on (each child is limber enough), but they never lose their grip. In what percent of all possible cases is it true that, when two children standing next to each other lose their grip, the ten children find themselves forming an unbroken chain?

Gy. 3280. Let p and q be positive real numbers whose reciprocals add up to 1. Prove that

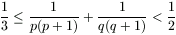and .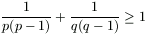

Proposer: S. Róka, Nyíregyháza

Gy. 3281. In a rectangular box, the lengths of the three edges starting at the same vertex are prime numbers. It is also given that the surface area of the box is a power of a prime. Prove that exactly one of the edge-lengths is a prime number of the form 2^k-1. 

Proposer: Á. Kovács, Budapest

Gy. 3282. Let a, b and c denote the sides of a triangle. Prove that

.

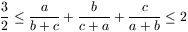Is it possible that equality holds?

Gy. 3283. On two sides of a right triangle, one of which is the hypotenuse, squares are built externally and a point M is constructed according to Figure 1. Prove that M is incident to the perimeter of the square inscribed into the triangle (see Figure 2).

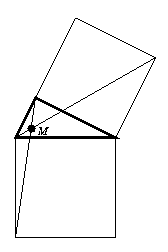Figure 1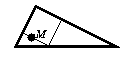

Figure 2

Gy. 3284. Assume that an arc of a circle halves the area of another circle k. Prove that the length of the arc is greater than the diameter of k.

Gy. 3285. What kind of rhombus has the property that there can be found two different parallelepipeds whose faces are all congruent to this rhombus? 

Proposer: K. Peták, Szolnok

New problems in May 1999

F. 3286. Find the values of t for which the binary operation, defined on positive numbers by 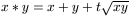is associative.

F. 3287. A partition of a set is obtained by any representation of the set as the union of pairwise disjoint subsets. Prove that a set of n elements has no more than n! partitions.

Proposer: S. Róka, Nyíregyháza

F. 3288. We have p^k|n! for some positive integers n, k and prime number p. Prove that n! is divisible by (p!)^k, too.

F. 3289. A point P and distances a, b and c are given. Construct an equilateral triangle such that the segments connecting P with the vertices of the triangle have length a, b and c, respectively.

F. 3290. Prove that the points, given by their coordinates as A(1, 0, 2), B(4, 3, -1), C(0, 3, -1), D(5, -2, 4), lie in the same plane. Find, moreover, the area of the convex quadrilateral determined by these four points.

F. 3291. Prove that any equilateral lattice polygon has an even number of edges.

Proposer: I. Z. Ruzsa, Budapest

New advanced problems in May 1999

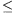N. 211. Count those n-term sequences of positive integers in which the number of terms greater than i is at most n-i, for each 1in.

N. 212. Determine those pairs of positive integers a and n for which each prime divisor of 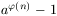also divides n.

N. 213. Let p_n(x)=a_n,0+a_n,1x+...+a_n,nxⁿ denote the unique polynomial, of degree at most n, whose values at 2⁰, 2¹, ..., 2ⁿ are 0, 1, ..., n, respectively. Find, for any positive integer k, the limit .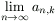

N. 214. Consider the parabola y=x². Suppose that two tangents are drawn to the parabola from a point P in the plane. Denote by Q_P and R_P, respectively, the points of contact, and by l(Q_P, R_P) the length of the arc of the parabola connecting Q_P and R_P. Find the locus of points P for which PQ_P+PR_P-l(Q_P, R_P) is constant.