Az 1999. szeptemberi számban kitűzött B-jelű matematika feladatok megoldásai

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

B. 3292. A család a két gyerekre bízta a felújítandó konyha kövének kiválasztását. Egyiküknek a baloldalon, másikuknak a jobboldalon látható színezés tetszik jobban. Végül úgy döntenek, azt választják, amelyikben több a barna szín. Melyiket választották? (3 pont)

 

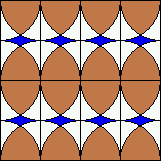
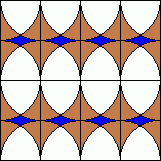
Megoldásvázlat. A jobboldali csempe barna darabjai belepakolhatók a baloldali csempe barna részeibe az ábra szerint:

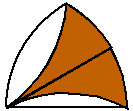
Ezért a baloldali csempén nagyobb a barna terület.

Megjegyzés. A barna területeket expliciten ki is lehet számolni. Ha a csempe oldala egységnyi, akkor a bal- illetve jobboldali csempén a barna rész területe 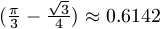illetve 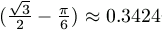egység.

B. 3293. Az a és b pozitív egész számokra teljesül, hogy 34a=43b. Mutassuk meg, hogy a+b összetett szám. (3 pont)

Javasolta: Róka Sándor, Nyíregyháza

1. megoldásvázlat. A 34 és a 43 relatív prímek. Ezért, ha 34a osztható 43-mal (hiszen egyenlő 43b-vel), akkor a is osztható 43-mal, vagyis a=43d egy alkalmas d pozitív egész számmal. Ekkor b=34a/43=34d és a+b=43d+34d=77d.

2. megoldásvázlat.

34(a+b)=34a+34b= 43b+34b=77b,

ezért a 34(a+b) szám osztható 77-tel. a 34 és a 77 relatív prímek, ezért ez azzal ekvivalens, hogy a+b osztható 77-tel. Tehát az a+b szám 7-tel és 11-gyel is osztható.

B. 3294. A táblára felírtuk az 1, 2, 3, ..., 20 számokat. Letörlünk közülük két számot, a-t és b-t, s helyettük felírjuk az ab+a+b számot. Ezt az eljárást 19-szer elvégezve milyen szám maradhat a táblán? (4 pont)

Javasolta: Róka Sándor, Nyíregyháza

Megoldásvázlat. Mint könnyen ellenőrizhető,

(a+1)^.(b+1)=(ab+a+b)+1.

Emiatt, ha a táblán levő számok a₁, a₂,..., akkor az S=(a₁+1)(a₂+1)... kifejezés értékét vizsgálva, az a műveletek során változatlan marad. Tehát a megmaradó szám: 2^.3^....^.21-1=21!-1.

B. 3295. Egy háromszög súlypontján átmenő egyenesek közül melyek felezik a háromszög területét? (4 pont)

Javasolta: Bogdán Zoltán, Cegléd

Megoldásvázlat. A súlyponton átmenő egyenesek közül csak a súlyvonalak felezik a háromszög területét.

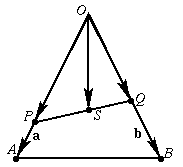
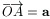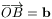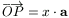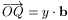Tegyük fel, hogy felezi az OAB háromszög területét egy egyenes, ami átmegy az S súlyponton, és metszi az OA és OB oldalakat a P illetve Q pontokban. Legyen , , és , ahol x és y alkalmas valós számok. Mint ismeretes, .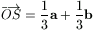

A 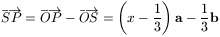és 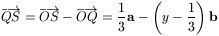vektorok párhuzamosak, ezért

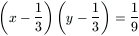.   (1)

Az, hogy a PQ egyenes felezi a háromszög területét, azzal ekvivalens, hogy

xy=.   (2)

Az (1) és (2) egyenletekből álló egyenletrendszernek két megoldása van: x=1 és y=, illetve x= és y=1. Ez pedig éppen az A-ból illetve B-ből induló súlyvonalakat jelenti.

B. 3296. Baloldalt egy sáska, középen egy szöcske, jobboldalt egy tücsök ül egy hosszú, egyenes árokban. Időnként valamelyik átugorja egyik szomszédját. Előfordulhat-e, hogy 1999 ugrás után a kiinduló sorrendben ülnek, ha végig csak az árokban (egy egyenes mentén) ugrálnak? (4 pont)

Javasolta: Róka Sándor, Nyíregyháza

Megoldásvázlat. Az egyszerűség kedvéért jelöljük a három rovart A, B, C-vel. Osszuk a lehetséges sorrendeket az alábbi két csoportba:

I.	II.
ABC BCA CAB	ACB CBA BAC

Könnyen ellenőrizhető, hogy egy-egy ugrás során az I. csoportba tartozó sorrendekből egy olyan sorrend jön létre, ami a II. csoportba tartozik, és fordítva. Ezért csak páros számú lépésben lehet az eredeti sorrendhez visszajutni, páratlan sok - például 1999 - lépésből ez lehetetlen.

Megjegyzés. Tetszőleges n pozitív egészre n elem, mondjuk az 1,2,...,n számok permutációit két csoportba, az úgynevezett páros és páratlan permutációkra lehet bontani.

Egy tetszőleges a₁,a₁,...,a_n permutációhoz keressük meg az összes olyan i<j számpárt, amelyre a_i>a_j. Az ilyen párok számát hívjuk a permutáció inverziószámának. Ha az inverziószám páros, akkor a permutációt páros permutációnak nevezzük, ellenekező esetben pedig páratlan permutációnak.

Ha egy permutációban két tetszőleges elemet (nem feltétlenül szomszédosakat!) felcserélünk, akkor a permutáció paritása megváltozik.

A permutációk paritásának vizsgálatával 3 helyett akárhány állatra is megoldható a feladat.

B. 3297. Egy derékszögű háromszög befogói a és b, átfogója c. Bizonyítsuk be, hogy 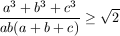. (4 pont)

Javasolta: Paulovics Illés

1. megoldásvázlat. Szorozzunk be a nevezővel, és rendezzük a baloldalra azokat a tagokat, amelyekben c szerepel; emeljünk négyzetre, és helyettesísünk be c² helyére a²+b²-et:

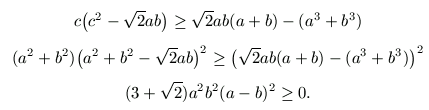
(Természetesen, ha az első sor jobboldalán negatív szám áll, akkor a négyzetreemelésre nincs szükség.)

2. megoldásvázlat.

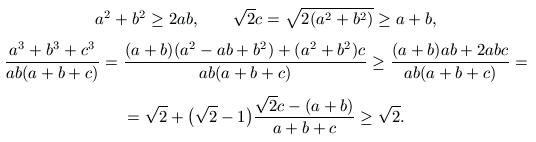
B. 3298. Egy háromszög alapú gúla oldalélei egységnyi hosszúságúak, az oldalélek által bezárt szögek 60^o, 90^o illetve 120^o. Mekkora a gúla térfogata? (4 pont)

Javasolta: Vajda Szilárd, Kolozsvár

Megoldásvázlat. Az alapélek könnyen adódnak: a, a, a. Ezek éppen egy derékszögű háromszöget határoznak meg. A testmagasság talppontja az alaplap köré írható kör középpontja, tehát az a hosszúságú oldal felezőpontja. Így az könnyen meghatározható: m=a/2.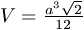

B. 3299. Egy R sugarú kerek asztalon elhelyeztünk n darab r sugarú pénzérmét úgy, hogy minden érme egy teljes lapjával az asztalon fekszik. Az asztalra újabb érme már nem helyezhető el. Mutassuk meg, hogy 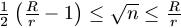. (5 pont)

Javasolta: Róka Sándor, Nyíregyháza

Megoldásvázlat. A pénzérmék összterülete kisebb az asztal területénél: n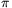^..r²<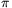^.R², innen 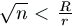. Most duplázzuk meg mindegyik érme sugarát, így ezek lefedik az R-r sugarú asztalt (ellenkező esetben el tudnánk helyezni még egy érmét az R sugarú asztalon), tehát n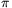^..(2r)²>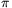^.(R-r)², amiből .

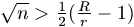B. 3300. Egy konvex poliéder egyik lapjának csúcsait pirosra, a többi csúcsot pedig kékre színeztük. Bizonyítsuk be, hogy van olyan kék csúcs, amelyből legfeljebb 5 él indul ki, vagy pedig van olyan piros csúcs, amelyből legfeljebb 3 él indul ki. (5 pont)

1. megoldásvázlat. Legyen a piros és kék csúcsok száma C_p illetve C_k, az élek száma E, a lapok száma L. A poliédertételből

C_p+C_k+L=E+2.   (1)

A lapok oldalszámának összege egyenlő az élek számának kétszeresével. Van egy C_p oldalú lap és további L-1 darab legalább háromoldalú lap, ezért

2E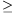C_p+3(L-1).   (2)

Legyen a legkisebb piros fokszám f_p, a legkisebb kék fokszám f_k. A csúcsok fokszámának összege szintén 2E, ezért

2E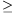C_p^.f_p+C_k^.f_k.   (3)

(1)-ből kifejezve L-et és beírva (2)-be,

2C_p+3C_k-3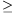E.   (4)

Ezt beírva (3)-ba,

C_p(4-f_p)+C_k(6-f_k)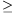6,

amiből következik, hogy f_p<4 vagy f_k<6.

2. megoldásvázlat. Tükrözzük a poliédert a piros lapra, és illesszük össze a poliédert a tükörképével. Az új poliéder is gömbbé deformálható, tehát - mint ismeretes - van legfeljebb ötödfokú c csúcsa. Ha c kék, akkor találtunk legfeljebb ötödfokú kék csúcsot. Ha c piros, akkor belőle két él piros csúcsba fut, a továbi élek fele eredeti, másik fele tükörkép kék csúcsba fut, ezért az eredeti kék csúcsba futó élek száma 1, tehát c eredetileg harmadfokú volt.

B. 3301. Egy H halmaz elemeinek száma: |H|=n. Mutassuk meg, hogy

.

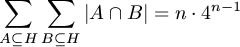(5 pont)

Javasolta: Róka Sándor, Nyíregyháza

1. megoldásvázlat. Nézzük meg, hogy egy elemet hányszor számolunk az összegzéskor! Annyiszor, ahány halmazpár metszetében szerepel. Mivel rajta kívül a H halmazban n-1 elem van, és (2^n-1)²=4^n-1 halmazpár hozható létre ebből az n-1 elemből, ezért ez az elem 4^n-1 halmazpár metszetében szerepel. Mivel H-ban n elem van, ezért az összeg n^.4^n-1.

2. megoldásvázlat. Egy n elemű halmaznak összesen 2ⁿ részhalmaza van, ezért a részhalmaz-párok száma 2^n.2ⁿ=4ⁿ. A részhalmazpárokat rendezzük 4-es csoportokba: 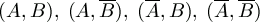. Ezen csoportok száma: 4ⁿ/4=4^n-1. egy ilyen csoportban a metszetek elemszámának összege n. Emiatt a kérdéses összeg: n^.4^n-1.

Megjegyzés:. Ha az összegzésben az A=B eseteket kizárjuk, akkor az n^.4^n-1 érték 2ⁿ-nel csökken.