Az 1999. októberi számban kitűzött C-jelű matematika gyakorlatok megoldása
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
C. 550. Egy horgász a napi zsákmánya össztömegének 35%-át kitevő három legnagyobb halat a mélyhűtőbe tette. A három legkisebb halat, amelyek együttesen a megmaradt rész 5/13-át tették ki, elvitte a macska, a többit pedig megfőzték ebédre. Hány halat fogott a horgász?
Javasolta: Dobos Sándor, Budapest
Megoldásvázlat.Ha a zsákmány össztömegét M jelöli, akkor a
mélyhűtőbe került 0.35M, amit a macska elvitt, az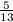 
(M-0.35M)=0.25M,
amit ebédre megfőztek, az pedig 0.4M. Ez legalább 4 halat
jelent, hiszen bármely 3 hal össztömege csupán 0.35M. Ha
legalább 5 hal lenne, akkor azok közül lenne 3, melyek együttes tömege
legfeljebb 
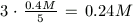lenne, ám már a 3
legkisebb hal is ennél többet tett ki. Vagyis ebédre 4 hal jutott, a
horgász pedig összesen 3+3+4=10 halat fogott.
C. 551. Határozzuk meg az x2+y2=x, 2xy=y egyenletrendszer összes megoldását.
Javasolta: Fried Ervin, Budapest
Megoldásvázlat.A 2. egyenletet átrendezve (2x-1)y=0 adódik, vagyis x=1/2 vagy y=0 kell, hogy teljesüljön. Ezt az 1. egyenletbe beírva, az első esetben y2=1/4, a második esetben x2=x, x(x-1)=0 adódik. Mindkét egyenletnek egyszerre tehát csak a következő 4 számpár tehet eleget: x1=1/2, y1=1/2, x2=1/2, y2=-1/2, x3=0, y3=0, x4=1, y4=0, melyek mindegyike valóban az egyenletrendszer megoldása.
C. 552. Az ábrán látható két kör középpontja 5 cm-re van egymástól, sugaraik hossza 3 cm és 4 cm. Mekkora a két satírozott terület különbsége?
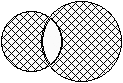
Megoldásvázlat. Jelölje a két kör közös részének területét
T, a két 'félhold' alakú rész területét pedig
T1, illetve T2, T1<T2. Ekkor a keresett különbség a kör
területképlete alapján T2-T1=(T2+T)-(T1+T)=(4 cm)2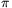
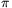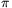-(3 cm)2=(7) cm2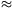
21.99 cm2, függetlenül a körök középpontjainak
távolságától.
C. 553. Egy 20 cm magas, 10 cm átmérőjű henger "meghízott". Magassága és alapjai nem változtak, alkotója viszont 1 mm-rel megnyúlt, és így két egybevágó csonkakúppá formálódott. Hány százalékkal nőtt a henger térfogata?
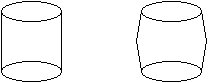
Megoldásvázlat. A henger alapkörének sugara r=5 cm,
magassága 2h=20 cm. A csonkakúp alakú részek magassága
h, alkotója a=
[2h+0.1 cm]=10.05 cm, fedőkörének
sugara r, alapkörének R sugarára pedig a Pitagorasz
tételből (R-r)2+h2=a2,
(R-r)2=(a+h)(a-h)=1.0025 cm2, ahonnan R-r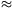1 cm, R=6cm adódik, utóbbira
kb. 0.02% pontossággal. A henger térfogata 2hr2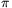, a két
csonkakúp együttes térfogata pedig 2.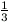
h(R2+Rr+r2)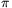, melyek
aránya 
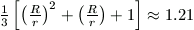. A henger térfogata tehát
kb. 21%-kal nőtt meg.
C. 554. Mutassuk meg, hogy van olyan a szám, hogy log2x+log3x=logax teljesül minden pozitív x-re.
Megoldásvázlat.Áttérve mindenhol a 2 alapú logaritmusra,
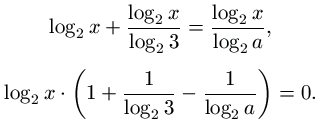
Ez pontosan akkor teljesül minden x-re, ha
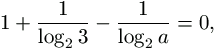
azaz
