New exercises and problems in Mathematics
October 1999
Please read The Conditions of the Problem Solving Competition.
 |
New exercises in October 1999 |
C. 550. An angler went fishing one day. When he returned he put the three largest fish, which comprised 35% of the total mass of the fish he caught, into the freezer. The three smallest fish that formed 5/13 of the remaining part were taken away by the cat, and the rest was cooked for dinner. How many fish did the angler catch that day?
Proposed by S. Dobos, Budapest
C. 551. Find all solutions of the following system of equations: x2+y2=x, 2xy=y.
Proposed by E. Fried, Budapest
C. 552. The circles depicted on the figure have radii 3 cm and 4 cm, respectively, their centres are 5 cm apart. Find the difference between the areas of the two shaded regions.
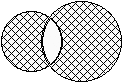
C. 553. A cylinder of diameter 10 cm and height 20 cm went under the following deformation. Its bases and its height remained the same while its generators increased by 1 mm, and thus it took the shape of two congruent frustum of cones joined at their bases. In what proportion did the volume of the body increase?
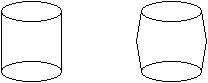
C. 554. Prove that there exists a number a such that log2x+log3x=logax holds for every positive number x.
 |
New problems in October 1999 |
B. 3302. Eight people are waiting in a queue at a box office, in some order. Each of them wants to buy a 10 dollar ticket. Four of them have only 10 dollar notes while the others have 20 dollar notes only. Consider all possible orders of the eight people. Assuming that there is no cash at the box office in the beginning, determine the proportion of those orders in which the cashier can issue the tickets without getting to any problem. (3 points)
B. 3303. A strip of paper, 5 cm wide, is folded without creasing according to the figure.
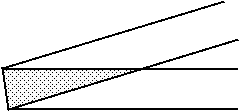
How small can the shaded area, which the strip covers twice, be? (4 points)
B. 3304. Is it possible to assign the numbers 1, 2, ..., 11, 12 to the edges of a cube such that the numbers assigned to the edges starting at a vertex is the same for each vertex of the cube? (4 points)
Proposed by G. Reményi, Budapest
B. 3305. Determine the value of the real parameter N such that the equation
2x2+4xy+7y2-12x-2y+N=0
has exactly one solution (x,y). (4 points)
B. 3306. In a triangle ABC of unit area, D and E denote the points which trisect side AB, the midpoint of side AC is denoted by F. Lines FE and FD intersect line CB in G and H, respectively. Determine the area of triangle FGH. (3 points)
B. 3307. The Figure shows a square. PA=AB=BC=CD=DE. What is the sum of angles MAN, MBN, MCN, MDN, MEN shown in the diagram? (3 points)
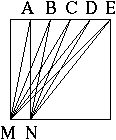
Russian competition problem
B. 3308. Two prime numbers which differ by 2 are called twin primes. Consider twin primes whose sum is a power of a prime. How many such pairs can be found? (4 points)
Proposed by Á. Kovács, Budapest
B. 3309. On each face of a cube, consider those points which divide a midline of the face in a ratio 1:3. How does the volume of the polyhedron determined by these points relate to the volume of the cube? (4 points)
B. 3310. Prove that the curve of equation (x2+y2)3=27x2y2 is contained in a square of side 4. (5 points)
B. 3311. If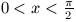 
, prove that
.
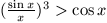(5 points)
Based on a problem proposed by Á. Kovács, Budapest
 |
New advanced problems in October 1999 |
A. 218. Find all continuous functions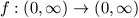 
which satisfy
.
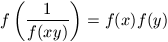A. 219. A set H consists of 2n points in the plane, no three collinear. Let P and Q denote any two distinct points of H. Segment PQ is called a halving segment if the same number of points of H lie on each side of line PQ. Assuming that H has exactly n halving segments, prove that any two such segments intersect.
Proposed by J. Solymosi, Budapest
A. 220. Given any positive integer n in decimal system, denote by S(n) the sum of its digits. Prove that
.
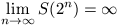Send your solutions to the following address:
KöMaL Szerkesztőség (KöMaL feladatok), Budapest Pf. 47. 1255, Hungary
or by e-mail to: megoldas@komal.elte.hu.