 |
Exercises and problems in Physics |
Please read The Conditions of the Problem Solving Competition.
New experimental problem:
M. 210. A test tube with some ballast at its bottom (water, shots,
sand, etc.) floats in water in a vertical position, in a large
graduated cylinder. When the test tube is slightly lifted and
released, it makes vertical damped oscillations. Measure the period
T of the oscillations (with different quantities of ballast)
and calculate the value of the quantity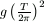 
. Compare x with the length of the test tube
immersed in water when the tube is at rest. (6 points)
New problems:
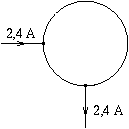
P. 3284. A closed ring made of some metal wire has a piece of wire soldered to each end of a quarter cycle of the ring as shown in the figure. Connecting these pieces of wire to a current supply, a current of 2.4 A starts flowing. What are the separate resistances of the quarter and the three-quarter cycles, if a pd. of 3.6 V is measured between the soldering points? What is the power taken up by the metal ring? (3 points)
P. 3285. A balloon with a mass of 7.3 kg, filled with helium gas at a temperature of 23o C, floats in the air as a sphere with a diameter of 2.4 m (it does neither rise, nor sink). The density of air around it is 1.19 km/m3.
What is the pressure of the helium gas? (4 points)
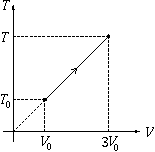
P. 3286. Silvia asks her friend Julia for help through the Internet, to solve the following physics problem:
"The figure represents some equilibrium process of n moles of monatomic ideal gas. How much heat does the gas take up during the process?"
Unfortunately, it turned out later that Silvia had typed wrong data on the vertical axis. The correct figure has symbols p instead of T.
How many times is the correct result greater than what Julia first calculated, assuming that the initial temperature of the gas is T0 in the correct figure as well? (4 points)
P. 3287. A stone is thrown horizontally with initial velocity v0. What is the time dependence of the angular velocity of this velocity vector? (5 points)
P. 3288. What is the maximum starting acceleration - on
level ground - of a motorcycle with a very strong engine if the wheel
base is l, the height of the centre of gravity is h and
the coefficient of friction between the wheels and the ground i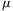s 
? The moment of inertia of the wheels is
small, the load on the wheels is identical in equilibrium. (5 points)
P. 3289. There are two electric dipoles in vacuum, at a distance of 3 m from each other, with respective electric dipole moments of 6.10-6 C m and 2.10-7 C m. (The dipoles can be approximated as pairs of charges.) What are the minimum and maximum values of the interaction energy between the two dipoles? (The point-like charges forming the dipoles are in both cases in one straight line.) (6 points)
P. 3290. A proton beam passes first through a 4 cm wide, homogeneous magnetic field with induction B1=0.2 T, and then through a second, also 4 cm wide, homogeneous magnetic field joining the first field, but with induction B2=0.4 T. The B-lines of the two fields are parallel and point into the same direction; the initial velocity of the protons is perpendicular both to the B-lines and to the limiting surface of the magnetic fields.
What accelerating voltage is required so that the protons can penetrate through both magnetic fields? (4 points)
P. 3291. What is the difference in percentage between the wavelength of the smallest frequency visible light emitted by deuterium and hydrogen atoms? (5 points)
P. 3292. Sometimes, interesting colourful streaks can be observed on a transparent plastic ruler lying on a table by the window. Give an explanation to the phenomenon. (5 points)
P. 3293. There is a body of mass m at the bottom of a thin and narrow tyre of mass m and radius r standing on a level table. The small body is started with a small, horizontal initial velocity v0 in the plane of the tyre. How does the centre of the tyre move afterwards? (Friction is negligible everywhere.) (6 points)