New exercises and problems in Mathematics
November 1999
Please read The Conditions of the Problem Solving Competition.
 |
New exercises in November 1999 |
C.555. Find the smallest integer which can be expressed as the sum of two distinct positive squares in two different ways.
C.556. A running competition is organized in five rounds. There are 50 contestants whose times are recorded in each round. The overall result is then determined by adding up the results obtained in the five rounds. Suppose that Bob finishes 10th in each round. Is it possible that he will have
- (a) the best
(b) the worst overall result?
C.557. Prove that there is no sequence consisting of at least two consecutive odd positive integers whose sum is a prime number.
Proposed by Sz. Vajda, Kolozsvár
C.558. In an nxn square grid, determine the number of such squares whose vertices are grid points and whose edges are parallel to the lines of the grid.
C.559. A cone shaped container, with its apex pointing downwards, is partly filled with water such that the surface of the water is 100 mm above the bottom of the container. When the container is closed and turned upside down, the water inside is only 20 mm deep. Determine the altitude of the cone.
Proposed by L. Koncz, Budapest
 |
New problems in November 1999 |
B.3312. Adding up the digits of his year of birth, Sylvester noticed that the result is the very number formed by the last two digits of the year of birth of his grandfather. Moreover, the last two digits of Sylvester's year of birth form his grandfather's present age. How old is Sylvester? (3 points)
Proposed by B. Nyul, Debrecen
B.3313. A rhombus ABCD is divided into two
equilateral triangles by its diagonal BD. Points P and
Q lie on segments AD and CD, respectively, such
that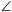 
PBQ=60o. Find the measure of the remaining two angles
of triangle PBQ. (3 points)
B.3314. Is it possible to assign the numbers 1,2,3,...,11,12 to the edges of a regular octahedron such that the numbers assigned to the edges starting at a vertex is the same for each vertex of the octahedron? (3 points)
Proposed by G. Reményi, Budapest
B.3315. Find a function f of the form f(x)=ax which is a `good' approximation for the function g(x)=x2 at the places x=0.1,0.2,0.3,0.4,0.5 in the following sense: the largest of the values |f(x)-g(x)| calculated at these places should be as small as possible. (4 points)
Proposed by G. Bakonyi, Budapest
B.3316. P denotes any point inside a triangle ABC. Lines AP and BP intersect the opposite sides of the triangle at points D and E, respectively. Prove 1/AP=1/AD+1/AC, provided that AP=BP and BE=CE. (4 points)
Proposed by H. Lee, Korea
B.3317. Solve the equation
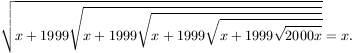
(4 points)
Proposed by Z. Hans, Nagykanizsa
B.3318. Circles k1 and k2, each of unit radius, touch at a point P. A line tangent to each circle, not passing through P, is denoted by e. Let, for i>2, ki denote the circle, different from ki-2, which is tangent to each k1,ki-1 and e. Determine the radius of k1999. (5 points)
B.3319. It is known that of all polygons determined by four points lying in a given circle, the inscribed squares possess the largest area. Is it also true that among all polyhedra determined by eight points on a given sphere, the largest volume belong to the inscribed cubes? (4 points)
B.3320. Solve the equation
xx1/2=1/2.
(5 points)
Proposed by L. Lovrics, Budapest
B.3321. There is given a convex polygon K in the plane. Prove that six congruent copies of K can be arranged around K such that each shares a common boundary point with K, but the interiors of the seven polygons are mutually disjoint. (5 points)
 |
New advanced problems in November 1999 |
A.221. Consider a square N whose vertices have
coordinates (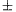
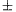1999; 1999). Let H denote the triangle with vertices
(-1; 0), (0; -1) and (1; 1). How many non-overlapping translated
copies of H can be packed into N?
Proposed by Gy. Pap, Debrecen
A.222. Integers a,b,c have highest common factor 1. The triplet a,b,c may be altered into another triplet such that in each step one of the numbers in the actual triplet is increased or decreased by an integer multiple of another element of the triplet. Is it true that, no matter how the numbers a,b,c are given, the triplet (1,0,0) can be obtained in at most 10 steps?
Proposed by M. Abért, Budapest
A.223. Determine all real functions f which satisfy
f(x-f(y))=f(x+y1999)+f(f(y)+y1999)+1
for arbitrary real numbers x,y.
Send your solutions to the following address:
KöMaL Szerkesztőség (KöMaL feladatok), Budapest Pf. 47. 1255, Hungary
or by e-mail to: megoldas@komal.elte.hu.