 |
Exercises and problems in Physics |
Please read The Conditions of the Problem Solving Competition.
New experimental problem:
M. 211. Drops dripping from a slightly open water tap follow each other at seemingly even time intervals. Observe this phenomenon for a long period of time. How can you characterise the difference between the time intervals? (6 points)
New problems:
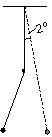 P. 3294. While swinging, a
thread pendulum runs into a nail each time it passes through its
vertical equilibrium position. The nail is exactly at the middle of
the thread. Give the difference in percentage between the time
necessary for the pendulum to swing back to its original position
(deviated by 2o) without and with the
nail. (3 points)
P. 3294. While swinging, a
thread pendulum runs into a nail each time it passes through its
vertical equilibrium position. The nail is exactly at the middle of
the thread. Give the difference in percentage between the time
necessary for the pendulum to swing back to its original position
(deviated by 2o) without and with the
nail. (3 points)
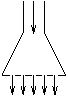 P. 3295. There are 18 circular
holes on a shower rose, with a diameter of 2 mm each. Water flows
at a speed of 0.5 m/s through the hose with a diameter of
10 mm. At what speed does water leave the holes? Does the kinetic
energy of water change? Does it increase or decrease? Give an
explanation. (4 points)
P. 3295. There are 18 circular
holes on a shower rose, with a diameter of 2 mm each. Water flows
at a speed of 0.5 m/s through the hose with a diameter of
10 mm. At what speed does water leave the holes? Does the kinetic
energy of water change? Does it increase or decrease? Give an
explanation. (4 points)
P. 3296. We have N different springs. Joining them in series results in a spring with a force constant of 52 N/m. When joined in parallel, the resultant force constant is 1872 N/m. What is the maximum possible value of N? (4 points)
P. 3297. Two 1 kg lead balls start towards each other due to gravity, in an environment devoid of other gravitational effects. How long does it take them to collide if the distance between the centres of mass of the balls was initially 1 metre? (The density of lead is 11 340 kg/m3.) (4 points)
P. 3298. Using a heat engine, some air with initially a volume of 7 litres, a pressure of 105Pa and a temperature of 0 o C is driven through a thermodynamic cycle consisting of two isobar and two isochore sections. During the cycle, the air is never colder than 0 o C, and the work done by the heat engine is 500 J. What can the maximum thermodynamic efficiency of this heat engine be? (5 points)
 P. 3299. One plate of a plane
capacitor has charge Q on it, the other one is uncharged. The
area of the plates is A, the distance between them is
d. a) What is the voltage of the capacitor? b)
What are the magnitude and the direction of the force acting on metal
plate no 2 when connected with a wire
to metal plate no 3 parallel to plate
no 2 and with the same area as the
latter (see the figure)? (4 points)
P. 3299. One plate of a plane
capacitor has charge Q on it, the other one is uncharged. The
area of the plates is A, the distance between them is
d. a) What is the voltage of the capacitor? b)
What are the magnitude and the direction of the force acting on metal
plate no 2 when connected with a wire
to metal plate no 3 parallel to plate
no 2 and with the same area as the
latter (see the figure)? (4 points)
P. 3300. Can the current flowing through a consumer (e.g. the electric starter of a car) fed by an accumulator be increased by connecting a galvanic cell with the same electromotive force as the accumulator, in parallel with the latter? (3 points)
P. 3301. A one-layer solenoid is made of some metal wire
with diameter d and specific resistance 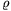 by coiling the wire onto a paper cylinder of radius
r, making (insulated) turns closely touching each other. The
solenoid is then connected to a current supply with internal
resistance R. How many turns should the solenoid have so that
the energy stored in the magnetic field be maximum? (
by coiling the wire onto a paper cylinder of radius
r, making (insulated) turns closely touching each other. The
solenoid is then connected to a current supply with internal
resistance R. How many turns should the solenoid have so that
the energy stored in the magnetic field be maximum? (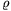 =1.78.10-8
=1.78.10-8 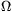 m;
R=1.2
m;
R=1.2 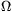 ;
d= mm; (r=3 cm. (5 points)
;
d= mm; (r=3 cm. (5 points)
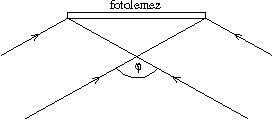 P. 3302. Holographic gratings
are made the following way: a parallel laser beam is divided into two
beams of identical intensity that are made to interfere at angle
P. 3302. Holographic gratings
are made the following way: a parallel laser beam is divided into two
beams of identical intensity that are made to interfere at angle 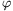 at the surface of a light-sensitised
plate. At what angle did the beams meet if light falling
perpendicularly onto the resulting optical grating is dispersed in
such a way that the complete secondary visible spectrum can just be
observed? The grating was made using a He-Ne laser with wavelength
at the surface of a light-sensitised
plate. At what angle did the beams meet if light falling
perpendicularly onto the resulting optical grating is dispersed in
such a way that the complete secondary visible spectrum can just be
observed? The grating was made using a He-Ne laser with wavelength
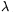 0=632 nm. (The visible spectrum extends from
380 nm to 760 nm.) (5 points)
0=632 nm. (The visible spectrum extends from
380 nm to 760 nm.) (5 points)
 P. 3303. A homogeneous rod of
mass m and length l is suspended onto a thread of length
l as shown in the figure. The upper end of the rod
receives a small thrust F
P. 3303. A homogeneous rod of
mass m and length l is suspended onto a thread of length
l as shown in the figure. The upper end of the rod
receives a small thrust F t. Describe the motion of the lowest point P
of the rod. (6 points)
t. Describe the motion of the lowest point P
of the rod. (6 points)

