New exercises and problems in Mathematics
December 1999
Please read The Conditions of the Problem Solving Competition.
 |
New exercises in December 1999 |
C. 560. A loaf of rye bread has a mass 25% smaller than a loaf of wheat bread, moreover, it is 20% more expensive. On the other hand, we always eat the whole loaf of rye bread, while 15% of the wheat bread becomes dry before we could finish up the whole loaf. Assuming the same consumption, determine, in percentage, how much more we spend if we consume rye bread instead of wheat bread.
C. 561. Find those prime numbers p for which p2+11 has exactly 6 positive divisors.
C. 562. Which positive integers n satisfy
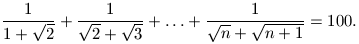
C. 563. In a circle of centre O and radius
r, let AB denote any chord shorter than the diameter of
the circle. Let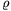 
denote the radius
of the circle inscribed the smaller sector of the the circle bounded
by the radii OA and OB. Express the length of AB
in terms of r and .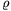
C. 564. The edges of a solid rectangular box are 26, 20 and 8 units long. Attached to each 26x8 face, build a tent roof whose lateral edges are 13 units long and whose `top' edge, parallel to its base, is 20 units long. Remove from the box the parts obtained by reflecting these tent roofs in their respective bases. Determine the volume of the solid which remains from the box.
 |
New problems in December 1999 |
B. 3322. Find the maximum number of parts into which the space can be divided by 4 concurrent planes. (3 points)
B. 3323. What is the longest interval in which the fraction of smallest denominator is 19/9999? (5 points)
B. 3324. How many ways are there to express 19991999 as the sum of consecutive natural numbers? (4 points)
Proposed by: T. Káspári, Paks
B. 3325. Prime numbers p1, p2, p3, p4 are called `quadruplets' if p1<p2<p3<p4 and p4-p1=8. Prove that if both p1, p2, p3, p4 and q1, q2, q3, q4 are quadruplets such that p1,q1>5, then p1-q1 is divisible by 30. Prove, moreover, that p1-q1 is never equal to 60. (3 points)
B. 3326. One face of a regular octahedron is projected perpendicularly to the plane of the opposite face. What proportion of the area of the opposite face is covered by the projection? (4 points)
Proposed by: M. Juhász, Budapest
B. 3327. Give an example of a nonzero polynomial of integral coefficients which admits cos 18o as a root. (4 points)
B. 3328. A convex polygon is `enlarged' by translating the line of each side outwards by 50 mm, perpendicularly to the given side. Show that the perimeter of the polygon is increased by more than 300 mm. (3 points)
Proposed by: Zs. Magyar, Budapest
B. 3329. A class of 31 students organize a Christmas party and they decide to present each other. Each of them draws the name of the one whom (s)he should present from a box. What is the probability that this drawing must be repeated because someone has drawn his or her own name? (4 points)
B. 3330. There are 1999 unit squares inside a square whose sides are 105 units long. Prove that one more unit square, disjoint from each of the others, can be placed inside the big square. (5 points)
B. 3331. In a certain school there are as many senior boys as girls therefore each senior student can have a partner for the dance at the graduation ball. Before arranging the couples, the girls are ranked by each boy, and vice versa. Prove that it is possible to arrange the pairs in such a way that there is not a boy and a girl who would rather dance with each other than with their actual partners. (5 points)
 |
New advanced problems in December 1999 |
A. 224. Prove that arbitrary positive numbers a1, a2, ..., an satisfy the following inequality
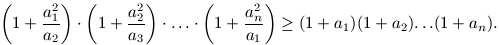
A. 225. Let S1 and S2 denote the sum of the numbers of odd resp. even divisors of the numbers 1, 2, ..., n. Prove that
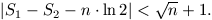
A. 226. Let k denote an arbitrary positive integer, and consider any graph whose vertex set is the set of positive integers and which does not contain a complete kxk bipartite subgraph. Prove that there exist arbitrarily long arithmetic progressions such that no two elements of the same progression are joined by an edge in the graph.
Proposed by: J. Solymosi, Budapest
Send your solutions to the following address:
KöMaL Szerkesztőség (KöMaL feladatok), Budapest Pf. 47. 1255, Hungary
or by e-mail to: megoldas@komal.elte.hu.