A 2000. januári B-jelű matematika feladatok megoldása
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
B. 3332. Az első n pozitív egész számot egy kör kerületén úgy szeretnénk elhelyezni, hogy bármely két szomszédos szám összege osztható legyen az óramutató járása szerint közvetlenül utánuk álló számmal. Milyen n-re lehetséges ez? (3 pont)
Tournament of Towns, 1999.
Megoldásvázlat. Először bebizonyítjuk, hogy nem állhat egymás után két páros szám. Legyen a, b és c három egymás utáni szám, és tegyük fel, hogy b és c páros. A feltétel szerint c osztója (a+b)-nek, ezért a+b és ezáltal a is páros. Azt kaptuk, hogy ha valahol egymás után két páros szám áll, akkor a közvetlenül előttük álló szám is páros. Visszafelé lépkedve pedig láthatjuk, hogy az összes szám páros, ami ellentmondás.
Másodszor azt bizonyítjuk be, hogy egy páros szám előtt két páratlan számnak kell állni. Legyen ismét a, b és c három egymás utáni szám, és tegyük fel, hogy c páros. Mint láttuk, b csak páratlan lehet. Viszont ezúttal is a páros c szám osztója (a+b)-nek, ezért a+b páros és a páratlan. Ha tehát c páros, akkor a és b páratlan.
Utóbbi eredményünkből következik, hogy a kör kerületén legalább kétszer annyi páratlan szám áll, mint páros. Viszont a páratlan számok száma legfeljebb csak 1-gyel nagyobb a páros számok számánál, ezért legfeljebb csak egy páros szám lehet; n értéke legfeljebb 3.

Ha n=1 vagy 3, akkor a kívánt felírás lehetséges, sőt lényegében egyértelmű; lásd a bal- és a jobboldali ábrát. (Az n=1 esetben mondhatjuk azt, hogy körben haladva az 1, 1, 1 számok egymás után következnek, és az 1+1=2-nek osztója az 1.) Ha n=2, akkor is csak egyféleképpen írhatók fel a kör körül az 1, 2 számok, de most az 1+2=3-nak nem osztója a 2.
Tehát n=1 és n=3 esetén írhatók fel a számok a kör kerületén a feltételeknek megfelelően.
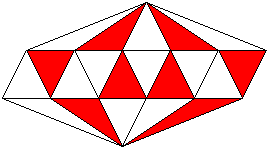
B. 3333. Egy ikozaéder néhány lapját pirosra festjük úgy, hogy két befestett lapnak nincs közös éle. Maximálisan hány lap festhető be ezzel a feltétellel? (3 pont)
Megoldásvázlat. Az ikozaédernek mind a 12 csúcsa öt-öt háromszögnek csúcsa. Az öt háromszög közül legfeljebb kettőt színezhetünk pirosra. Ezért a pirosra színezett háromszögeknek összesen legfeljebb 12x2=24 csúcsa lehet, vagyis a piros háromszögek száma nem lehet nagyobb 8-nál. Nyolc lapot viszont pirosra színezhetünk az ábra szerint.
B. 3334. Bizonyítsuk be, hogy egyetlen olyan számrendszer van, amelyben van olyan háromjegyű szám, amelyik kétszer akkora, mint az ugyanezekkel a számjegyekkel ugyanolyan sorrendben felírt tízes számrendszerbeli szám. (4 pont)
Javasolta: Gyanta Nándor, Budapest
Megoldásvázlat. Legyen az ismeretlen számrendszer alapszáma x, a háromjegyű szám jegyei a, b, c. Ezek egy 10-es számrendszerben felírt háromjegyű szám jegyei, ezért értékük legfeljebb 9 és a nem lehet 0. A feltétel szerint
ax2+bx+c=2(100a+10b+c);
(1) a(x2-200)+b(x-20)=c.
Ha x 14, akkor a baloldal
negatív, és (1) nem teljesülhet.
14, akkor a baloldal
negatív, és (1) nem teljesülhet.
Ha x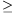 20, akkor
x2-200 és x-20 is
nemnegatív, x2-200
20, akkor
x2-200 és x-20 is
nemnegatív, x2-200 a(x2-200)+b(x-20)=c
a(x2-200)+b(x-20)=c 9. Ebből x2
9. Ebből x2 209 azaz
x
209 azaz
x 14, ami szintén ellentmondás.
14, ami szintén ellentmondás.
Végül, ha 15 x
x 19, akkor x2-200 pozitív, x-20 negatív, és
x2-200+9(x-20)
19, akkor x2-200 pozitív, x-20 negatív, és
x2-200+9(x-20) a(x2-200)+b(x-20)=c
a(x2-200)+b(x-20)=c 9. Ebből x2+9x-389
9. Ebből x2+9x-389 0
azaz x
0
azaz x 15. Ez a feltétel szerint
azt jelenti, hogy x=15.
15. Ez a feltétel szerint
azt jelenti, hogy x=15.
Az x=15 esetben három megoldás is van:
| a | b | c |
|---|---|---|
| 1 | 4 | 5 |
| 1 | 5 | 0 |
| 2 | 9 | 5 |
B. 3335. A K és L sokszögek úgy helyezkednek el a síkon, hogy csúcsaik nincsenek rajta a másik sokszög oldalegyenesein. Legfeljebb hány pontban metszik egymást az oldalak, ha K ötszög és
a) L háromszög;
b) L négyszög? (5 pont)
Megoldásvázlat. a) Egy egyenes egy a háromszögnek legfeljebb két oldalát metszheti. Ezért a K ötszög mindegyik oldalán legfeljebb két metszéspont lehet, K és L oldalai összesen tehát legfeljebb 10-szer metszhetik egymást. A 10 metszéspont lehetséges, például a baloldali ábrán látható módon.

b) Egy egyenes az ötszögnek nem metszheti mindegyik oldalát, mert valamelyik két szomszédos csúcs az egyenesnek ugyanarra az oldalára esik. Ezért az L négyszög mindegyik oldala legfeljebb 4-szer metszi a K ötszög oldalait; összesen legfeljebb 4x4=16 metszéspont lehet. A 16 metszéspont lehetséges, lásd a jobboldali ábrát.
B. 3336. Egy szabályos háromszöget a középpontja körül pozitív irányba elforgatunk először 3o-kal, azután tovább forgatjuk 9o-kal, majd 27o-kal, a k-adik lépésben 3k fokkal. Hányféle helyzetet vehet fel a háromszög az elforgatások eredményeképpen? (3 pont)
Megoldásvázlat. A háromszög két elforgatottja akkor esik egybe, ha az elforgatások szögének különbsége osztható 120 fokkal.
Ha n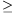 1, akkor 3n+3n+1+3n+2+3n+3=(3+9+27+81).3n-1=120.3n-1. Ezért bármelyik 4 szomszédos
elforgatás egymás utánja nem hoz létre új helyzetet. Csak a kiinduló
állapot és az első 3 elforgatott lesz különböző.
1, akkor 3n+3n+1+3n+2+3n+3=(3+9+27+81).3n-1=120.3n-1. Ezért bármelyik 4 szomszédos
elforgatás egymás utánja nem hoz létre új helyzetet. Csak a kiinduló
állapot és az első 3 elforgatott lesz különböző.
B. 3337. Adott egy parabola fókusza és két pontja. Szerkesszük meg a vezéregyenesét. (3 pont)
Megoldásvázlat. Legyen a fókuszpont F, a két megadott pont A és B.
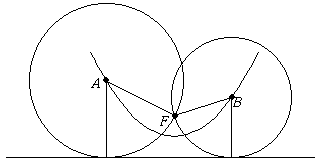
A vezéregyenes ugyanolyan távol van az A illetve B pontoktól, mint F. Rajzoljuk meg A és B körül azt a két kört, amely átmegy F-en. A vezéregyenes ennek a két körnek közös érintője.
A feladatnak általában két megoldása van.
B. 3338. Oldjuk meg a következő egyenletrendszert:
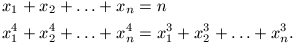 (4 pont)
(4 pont)
Javasolta: Ábrány Miklós, Ukrajna
Megoldásvázlat. Tetszőleges x valós számra
x4-x3-x+1=(x-1)2(x2+x+1)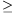 0,
0,
és egyenlőség csak x=1 esetén áll. Ezt az egyenlőtlenséget felírva az x1, ..., xn számokra és összeadva kapjuk, hogy
(x14+...+xn4)-(x13+...+xn3)-(x1+...+xn)+n=(x14+...+xn4)-(x13+...+xn3)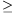 0,
0,
és egyenlőség csak x1=1; x2=1;...; xn=1 esetén teljesül. Tehát az eredeti egyenletrendszernek csak az x1=x2=...=xn=1 a megoldása.
B. 3339. Bizonyítsuk be, hogy egy gömbháromszög súlyvonalai egy pontban metszik egymást. (Egy gömb felszínén lévő A és B pontok gömbi összekötő egyenesének az A-t és B-t tartalmazó nem hosszabb főkörívet nevezzük.) (4 pont)
Megoldásvázlat. Legyenek a gömbháromszög csúcsi A,B,C, a gömb középpontja O. Legyen az AB ív felezőpontja F, az AB szakaszé G. Az O, G és F pontok egy egyenesen vannak. A gömbháromszög C-ből induló súlyvonala az az ív, amit a gömbfelületből az OCF sík kimetsz. Ez a sík az ABC háromszög síkját a CF szakaszban metszi, ami az ABC háromszög C-ből induló súlyvonala.

Hasonlóan láthatjuk, hogy az ABC gömbháromszög másik két súlyvonalának síkja az ABC háromszöget a másik két súlyvonalában metszi. mindhárom súlyvonal síkja illeszkedik tehát az ABC síkháromszög súlypontjára, tehát egy egyenesre illeszkednek. Ez pedig azt jelenti, hogy a gömbháromszög súlyvonalai is egy ponton mennek át, amely nem más, mint a síkháromszög súlypontjának vetülete a gömbfelületre.
B. 3340. Egy szabályos dobókockát 12-szer feldobva melyik esemény valószínűsége nagyobb?
a) Az első 6 dobás között lesz legalább egy 6-os.
b) A 12 dobás között lesz legalább két 6-os. (4 pont)
Megoldásvázlat. a) A lehetséges dobássorozatok száma
66. Ezek között 56 olyan eset van, amikor nincs 6-os. Annak
valószínűsége, hogy lesz legalább egy 6-os, 1-56/66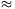 66,51%.
66,51%.
b) A lehetséges dobássorozatok száma 612. Ezek közül 512 esetben nincs 6-os, további 12.
511 esetben 1 darab 6-os van. A
keresett valószínűség 1-512/612-
12.511/612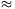 61,87%.
61,87%.
Az a) esemény valószínűsége nagyobb.
B. 3341. Az ABC háromszög A-ból induló magasságának talppontja D. Legyenek E és F egy, a D ponton átmenő egyenesnek olyan -- D-től különböző -- pontjai, amelyekre AE merőleges BE-re, AF merőleges CF-re. A BC és EF szakaszok felezőpontja M, illetve N. Bizonyítsuk be, hogy AN és MN merőlegesek. (5 pont)
X. Ázsiai Matematikai Olimpia feladata
Megoldásvázlat. Rajzoljuk meg az AB és az AC átmérőjű köröket. A merőlegességi feltételek szerint E illetve F ezeken a körökön van.
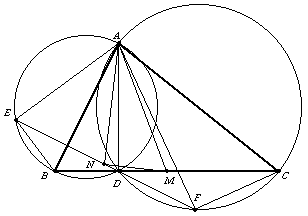
A kerületi szögek tételéből látható, hogy AEF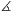 =ABC
=ABC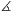 és AFE
és AFE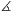 =ACB
=ACB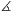 a
pontok elhelyezkedésétől függetlenül. Az ABC és AEF
háromszögek tehát hasonlóak, és a körüljárásuk is megegyezik. (Ez a
lépés hosszas diszkussziót igényel; külön-külön meg kell vizsgálni
azokat az eseteket, amikor a háromszög hegyes-, tompa- illetve
derékszögű, továbbá amikor E és F az AD
egyenesnek a B-vel illetve C-vel megegyező vagy azzal
ellentétes oldalán vannak.)
a
pontok elhelyezkedésétől függetlenül. Az ABC és AEF
háromszögek tehát hasonlóak, és a körüljárásuk is megegyezik. (Ez a
lépés hosszas diszkussziót igényel; külön-külön meg kell vizsgálni
azokat az eseteket, amikor a háromszög hegyes-, tompa- illetve
derékszögű, továbbá amikor E és F az AD
egyenesnek a B-vel illetve C-vel megegyező vagy azzal
ellentétes oldalán vannak.)
Tekintsük azt az A körüli forgatva nyújtást, ami az ABC háromszöget az AEF háromszögbe viszi. Ez a BC oldal felezőpontját, M-et az EF oldal felezőpontjába, N-be viszi. Ezért az ABE, AMN és ACF háromszögek hasonlóak; Az E, az N illetve F csúcsuknál derékszög van.

