 |
Exercises and problems in Physics |
Please read The Conditions of the Problem Solving Competition.
New experimental problem:
M. 214. Measure the freezing-point of a lean solution of alcohol in water as a function of the dilution. At what composition will the freezing-point be -18 Co? (6 points)
New problems:
 P. 3324. The mirrors of two
car headlights have been placed on top of each other, turned towards
each other, as shown in the figure. There is a stopper in the bottom
mirror but not in the top mirror, but it looks as if there were one in
the top mirror as well. Explain the phenomenon. (4 points)
P. 3324. The mirrors of two
car headlights have been placed on top of each other, turned towards
each other, as shown in the figure. There is a stopper in the bottom
mirror but not in the top mirror, but it looks as if there were one in
the top mirror as well. Explain the phenomenon. (4 points)
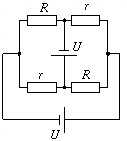 P. 3325. The circuit shown
in the figure is composed of two times two identical resistors and two
identical batteries. What current flows through the resistors
r? (R=20
P. 3325. The circuit shown
in the figure is composed of two times two identical resistors and two
identical batteries. What current flows through the resistors
r? (R=20 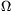 ,
r=10
,
r=10 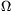 ,
U=10 V.) (4 points)
,
U=10 V.) (4 points)
P. 3326. A piece of ice floats in water in a vessel. Some oil is carefully poured onto it, enough to just cover it. The piece of ice slowly melts, while the temperature of the system remains constant. Does the level of the oil rise or sink in the vessel? Does the gravitational potential energy of the system increase or decrease? (5 points)
P. 3327. An astronaut on a space trip moves away from his space shuttle. He has two light, identical spring guns, capable of shooting two projectiles of identical mass. How can he obtain a higher speed: by shooting the two guns simultaneously or consecutively in the same direction? (Let for example the mass of one projectile equal one twentieth of the total mass of the astronaut and the two guns.) (5 points)
P. 3328. On which of several slopes of identical base but
different angles of inclination does a small body slide down in the
shortest time if the coefficient of dynamic friction is 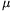 ? (5 points)
? (5 points)
P. 3329. Two small metal balls are suspended from the same point on threads of length l=0.5 m each. The mass of one of the metal balls is m=2 g, that of the other one is twice as large. The balls are given identical electric charges. What is this charge if the balls are at distance d=20 cm from each other in equilibrium? (5 points)
P. 3330. A soap bubble of radius r is blown in atmospheric pressure p0. When it is given electric charge Q, its radius increases to R. What is the surface tension of the solution of soap? (5 points)
P. 3331. Imagine that there is only a homogeneous sphere of
density 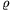 0 in space. The sphere starts expanding due to a
flash-explosion in such a way that the speed of any of its points is
initially v0(r)=H.r with
respect to its centre, where H is a value characteristic of the
expansion and r is the distance of the given point from the
centre of the sphere. What is the minimum value of H required
to maintain the eternal expansion of this sphere in spite of the
gravitational attraction? (5 points)
0 in space. The sphere starts expanding due to a
flash-explosion in such a way that the speed of any of its points is
initially v0(r)=H.r with
respect to its centre, where H is a value characteristic of the
expansion and r is the distance of the given point from the
centre of the sphere. What is the minimum value of H required
to maintain the eternal expansion of this sphere in spite of the
gravitational attraction? (5 points)
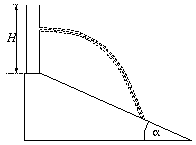 P. 3332. A cylindrical
vessel of height H stands on top of a long slope with angle of
inclination
P. 3332. A cylindrical
vessel of height H stands on top of a long slope with angle of
inclination 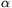 . The vessel is
filled with water to the brim. Where should a hole be drilled on the
side of the vessel so that the water flowing out reach the slope the
furthest possible? Represent the distance of the impact as a function
of the height of the hole for
. The vessel is
filled with water to the brim. Where should a hole be drilled on the
side of the vessel so that the water flowing out reach the slope the
furthest possible? Represent the distance of the impact as a function
of the height of the hole for 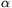 =15o and
=15o and 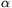 =45o. (6 points)
=45o. (6 points)
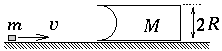 P. 3333. A body of mass
M with a half-cylindrical dent on one side stands on a
frictionless table, as shown in the figure. What is the minimum
initial speed v required for the body of mass m so that
it runs through the dent of radius R of the body of mass
M? (Friction is negligible everywhere.) (6 points)
P. 3333. A body of mass
M with a half-cylindrical dent on one side stands on a
frictionless table, as shown in the figure. What is the minimum
initial speed v required for the body of mass m so that
it runs through the dent of radius R of the body of mass
M? (Friction is negligible everywhere.) (6 points)
