New exercises and problems in Mathematics
March 2000
Please read The Conditions of the Problem Solving Competition.
 |
New exercises in March 2000 |
C.575. ``Well, I want you to answer me this. If two
stage-coaches leave Pozsony for Brassó every day, and as many leave
Brassó for Pozsony, and assuming that the journey takes ten days, then
how many coaches would you meet on the way if you travelled in one
stage-coach from Pozsony to Brassó?'' 
Proposed by K. Mikszáth, Fogaras
C.576. Find the smallest positive integer which, multiplied by 1999, yields a product whose last 4 digits are 2,0,0,1.
Proposed by M. Braun
C.577. Deep inside a drawer, there are 3 pairs of socks, somewhat different from each other. We try it three times to fish one sock out of the drawer. What is the probability that we end up with one sock of each pair after the 3 trials?
C.578. Consider the triangle whose vertices in the Cartesian system are A(2;-1), B(3;1) and C(21999;22000). Calculate the area of the triangle.
C.579. A circular disc is cut into two sectors along two of its radii. The two pieces are then turned into cone shaped funnels. Is it true that the largest total volume is obtained from two half discs?
 |
New problems in March 2000 |
B.3352. The number of the crew of a certain ship, multiplied
by one less the number of the crew exceeds, by 15, the product of the
age of the captain and the number two less the number of the
crew. What is the captain's name?  (3 points)
(3 points)
Repeta
B.3353. Determine the value of the following expression:
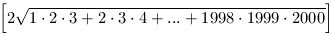
(4 points)
Proposed by M. Ábrány, Ukraine
B.3354. Two intersecting lines and a point P outside the lines are given in the plane. Construct points X and Y on the two lines, respectively, such that P is incident to the segment XY, and PX.PY is minimal. (5 points)
B.3355. Prove that a triangle has a right angle if and only if the product of two of its escribed circles equals to the area of the triangle. (4 points)
Proposed by B. Bíró, Eger
B.3356. Demonstrate that there are an infinite number of cases when the difference between the fourth powers of two consecutive integers can be written as the sum of two perfect sqares. (4 points)
B.3357. Is there any perfect square which has the same number of positive divisors of the form 3k+1 as of the form 3k+2? (4 points)
B.3358. Prove that among any 4 different real numbers there exist two, a and b such that
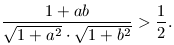
(5 points)
Proposed by J. Mezei, Vác
B.3359. The real roots x1, x2, x3 of the equation x3-3x-1=0 satisfy x1<x2<x3. Prove that x32-x22=x3-x1. (5 points)
Proposed by S. Mihalovics, Esztergom
B.3360. In a triangle ABC with centroid S, Let E and F denote the midpoints of sides AB and AC, respectively. Prove that the quadrilateral AESF is cyclic if and only if AB2+AC2=2BC2. (4 points)
Proposed by S. Kiss, Szatmárnémeti
B.3361. Two spheres G1 and G2 are given. Cubes K1 and K2 are inscribed into G1 and G2, respectively. Consider the 64 vectors whose starting points are the vertices of K1 and whose endpoints are the vertices of K2. Prove that the sum of these vectors does not depend on the position of the cubes within the spheres. (3 points)
 |
New advanced problems in March 2000 |
A.233. A sequence (an) is defined as follows: a0=a1=1, (n+3)an+1=(2n+3)an+3nan-1. Prove that each term of the sequence is an integer.
A.234. Any finite sequence of the letters A,B,C is called a word. A word can be transformed into an other word by the following two operations:
a) we choose any contiguous part of the word and double it, as in
the example BBCAC BBCABCAC;
BBCABCAC;
b) (the reverse of the first operation) if two consecutive
contiguous parts of the word are identical, we may omit one of them,
as in the example ABCABCBC ABCBC.
ABCBC.
Prove that any word can be transformed into a word of not more than 8 letters.
A.235. Let a be a fixed complex number. Find the locus of all complex numbers b for which there exist nonnegative real numbers x1,x2,...,xn and complex numbers z1,z2,...,zn of unit modulus such that x1+x2+...+xn=1, x1z1+x2z2+...+xnzn=a and x1z12+x2z22+...+xnzn2=b.
Send your solutions to the following address:
KöMaL Szerkesztőség (KöMaL feladatok), Budapest Pf. 47. 1255, Hungary
or by e-mail to: megoldas@komal.elte.hu.
